题目内容
已知数集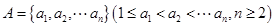 具有性质
具有性质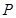 ;对任意的
;对任意的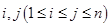 ,
,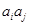 与
与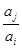 两数中至少有一个属于
两数中至少有一个属于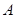 .
.
(Ⅰ)分别判断数集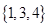 与
与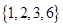 是否具有性质
是否具有性质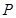 ,并说明理由;
,并说明理由;
(Ⅱ)证明: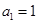 ,且
,且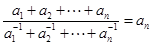 ;
;
(Ⅲ)证明:当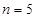 时,
时,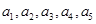 成等比数列..
成等比数列..
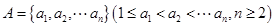 具有性质
具有性质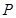 ;对任意的
;对任意的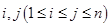 ,
,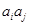 与
与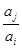 两数中至少有一个属于
两数中至少有一个属于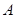 .
.(Ⅰ)分别判断数集
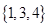 与
与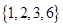 是否具有性质
是否具有性质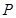 ,并说明理由;
,并说明理由;(Ⅱ)证明:
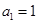 ,且
,且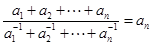 ;
;(Ⅲ)证明:当
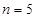 时,
时,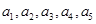 成等比数列..
成等比数列..(1)该数集不具有性质P (2)见解析 (3)见解析
【错解分析】本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、分类讨论等数学思想方法.本题是数列与不等式的综合题,属于较难层次题.
【正解】(Ⅰ)由于
 与
与 均不属于数集
均不属于数集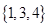 ,∴该数集不具有性质P.
,∴该数集不具有性质P.由于
 都属于数集
都属于数集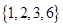 , ∴该数集具有性质P.(Ⅱ)∵
, ∴该数集具有性质P.(Ⅱ)∵ 具有性质P,∴
具有性质P,∴ 与
与 中至少有一个属于A,
中至少有一个属于A,由于
 ,∴
,∴ ,故
,故 .从而
.从而 ,∴
,∴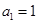 .
.∵
 , ∴
, ∴ ,故
,故 .
.由A具有性质P可知
 .又∵
.又∵ ,
,∴
 ,
,从而
 ,∴
,∴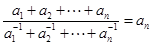 .
.(Ⅲ)由(Ⅱ)知,当
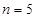 时,有
时,有 ,即
,即 , ∵
, ∵ ,∴
,∴ ,∴
,∴ ,由A具有性质P可知
,由A具有性质P可知 .由
.由 ,得
,得 ,且
,且 ,∴
,∴ ,∴
,∴ ,即
,即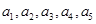 是首项为1,公比为
是首项为1,公比为 成等比数列.
成等比数列.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 }的公比
}的公比 , 已知
, 已知 =1,
=1, ,则{
,则{ ,则1+2+22+23+…+2n-1=
,则1+2+22+23+…+2n-1=

 的等差中项是
的等差中项是 ,一个等比中项是
,一个等比中项是 ,且
,且 则双曲线
则双曲线 的离心率为( )
的离心率为( )



 的通项公式
的通项公式 ,记
,记 ,试通过计算
,试通过计算 、
、 、
、 的值,推测出
的值,推测出 .
. 的通项公式是
的通项公式是 ,其前n项和是
,其前n项和是 ,则对任意的
,则对任意的 (其中
(其中 *),
*), 的最大值是 .
的最大值是 . 中
中 ,且
,且 ,则
,则 =
=  是各项为正数的无穷数列,
是各项为正数的无穷数列, 是边长为
是边长为 的矩形面积(
的矩形面积( ),则
),则 为等比数列的充要条件为
为等比数列的充要条件为 是等比数列。
是等比数列。 或
或 是等比数列。
是等比数列。 中,各项都是正数,而且
中,各项都是正数,而且 成等差数列,则
成等差数列,则 ( )
( )


