题目内容
已知函数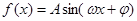

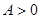 ,
,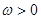 ,
,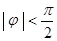
在一个周期内,当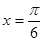 时,
时, 有最大值为
有最大值为 ,当
,当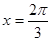 时,
时, 有最小值为
有最小值为  .
.
(1)求函数 表达式;(2)若
表达式;(2)若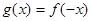 ,求
,求 的单调递减区间.
的单调递减区间.
(1)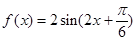 (2)
(2)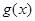 的单调减区间为
的单调减区间为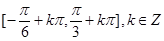 .
.
解析试题分析:(1)由函数 的最值可求得
的最值可求得 ,利用半个周期可求得
,利用半个周期可求得 ,最后再将点
,最后再将点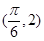 代入
代入 即可求得
即可求得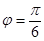 ,即函数
,即函数 的解析式可求出.
的解析式可求出.
(2)先求得函数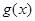 的解析式,再利用正弦型函数的单调性即可求得
的解析式,再利用正弦型函数的单调性即可求得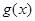 的单调减区间.
的单调减区间.
试题解析:(1) 当
当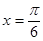 时,
时, 有最大值为
有最大值为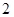 ,当
,当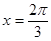 时,
时, 有最小值为
有最小值为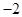 .
.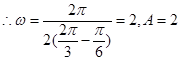 ,把点
,把点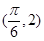 代入
代入 解得
解得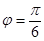 ,
,
所以函数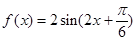
(2)由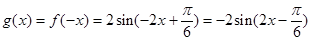 ,
,
由 可得:
可得:  ,
,
即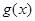 的单调减区间为
的单调减区间为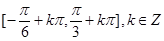 .
.
考点:三角函数解析式的求法;三角函数的性质.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
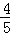 ,α为第三象限角.
,α为第三象限角.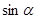 ,
, 的值;
的值;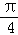 ),tan2α的值.
),tan2α的值. .
.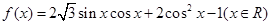 ,
,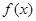 的最小正周期及在区间
的最小正周期及在区间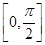 上的最大值和最小值;
上的最大值和最小值;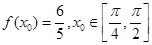 ,求
,求 的值.
的值. ,
, .
.  ;
; 有下列命题:①函数
有下列命题:①函数 的周期为
的周期为 ; ②直线
; ②直线 是
是 是
是 个单位,可得到
个单位,可得到 的图象.其中真命题
的图象.其中真命题 的序号是 .(把你认为真命题的序号都写上)
的序号是 .(把你认为真命题的序号都写上) 的顶点在坐标原点,始边写
的顶点在坐标原点,始边写 轴的正半轴重合,
轴的正半轴重合, ,角
,角 的终边与单位圆交点的横坐标是
的终边与单位圆交点的横坐标是 ,角
,角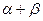 的终边与单位圆交点的纵坐标是
的终边与单位圆交点的纵坐标是 。
。 =
=  ,计算
,计算 的值为
的值为