题目内容
已知f(x)=x3-3ax2-bx(其中a,b为实数),
(Ⅰ)若f(x)在x=1处取得极值为2,求a、b的值;
(Ⅱ)若f(x)在区间[-1,2]上为减函数且b=9a,求a的取值范围.
(Ⅰ)若f(x)在x=1处取得极值为2,求a、b的值;
(Ⅱ)若f(x)在区间[-1,2]上为减函数且b=9a,求a的取值范围.
解:(Ⅰ)由题意可知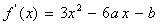 ,所以
,所以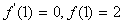 ,
,
即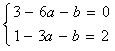 ,解得:
,解得: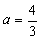 ,b=-5,
,b=-5,
此时,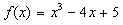 ,经检验,在x=1处有极小值,
,经检验,在x=1处有极小值,
故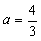 ,b=-5符合题意.
,b=-5符合题意.
(Ⅱ)若f(x)在区间[-1,2]上为减函数,则f′(x)≤0对x∈[-1,2]恒成立,
即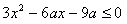 对x∈[-1,2]恒成立,
对x∈[-1,2]恒成立,
∴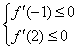 ,即
,即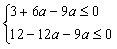 ,解得:a≥1,
,解得:a≥1,
∴a的取值范围是a≥1。
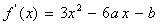 ,所以
,所以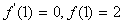 ,
,即
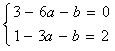 ,解得:
,解得: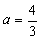 ,b=-5,
,b=-5,此时,
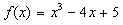 ,经检验,在x=1处有极小值,
,经检验,在x=1处有极小值,故
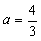 ,b=-5符合题意.
,b=-5符合题意.(Ⅱ)若f(x)在区间[-1,2]上为减函数,则f′(x)≤0对x∈[-1,2]恒成立,
即
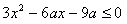 对x∈[-1,2]恒成立,
对x∈[-1,2]恒成立,∴
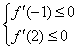 ,即
,即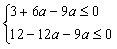 ,解得:a≥1,
,解得:a≥1,∴a的取值范围是a≥1。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目