题目内容
已知集合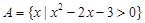 ,
,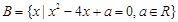 .
.
(1)存在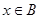 ,使得
,使得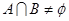 ,求
,求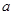 的取值范围;
的取值范围;
(2)若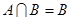 ,求
,求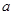 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)集合 ,
,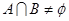 即为
即为 在
在 上有零点,利用二次函数的图象判断即得结果或转化为求函数
上有零点,利用二次函数的图象判断即得结果或转化为求函数 在
在 上的值域更为简单;(2)
上的值域更为简单;(2)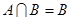 即
即 ,或
,或 的零点(一个或两个)都在
的零点(一个或两个)都在 内,结合二次函数的图象判断即得结果,数形结合的思想在解题中起到了重要的作用.
内,结合二次函数的图象判断即得结果,数形结合的思想在解题中起到了重要的作用.
试题解析:(1)由题意得 ,故
,故 ,解得
,解得 ① 2分
① 2分
令 ,对称轴为
,对称轴为 ,
,
∵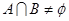 ,又
,又 ,
,
∴ ,解得
,解得 ② 5分
② 5分
由上①②得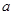 的取值范围为
的取值范围为 7分
7分
(2)∵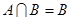 ,∴
,∴
当 ,即
,即 时,
时, 是空集,这时满足
是空集,这时满足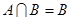 9分
9分
当 ,即
,即 ③
③
令 ,对称轴为
,对称轴为 ,∵
,∵ ,
,
∴ ,解得
,解得 ④
④
由③④得 , 12分
, 12分
综上得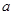 的取值范围为
的取值范围为 14分
14分
考点:一元二次方程、一元二次不等式和二次函数.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 ,设集合
,设集合 ,集合
,集合 ,若
,若 ,求实数a的取值范围.
,求实数a的取值范围.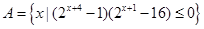 与
与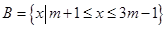 分别是函数
分别是函数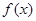 的定义域与值域.
的定义域与值域.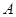 ;
;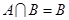 时,求实数
时,求实数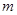 的取值范围.
的取值范围. 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 .
.
 ;
; ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围. ,B=
,B=

 ,求实数
,求实数 的取值范围.
的取值范围.  。
。 是空集,求
是空集,求 的取值范围;(2)若
的取值范围;(2)若 ,集合
,集合 .
. ,求
,求 ;
; ,求
,求 的取值范围.
的取值范围.