题目内容
(本题14分)
已知数列 的前
的前 项和为
项和为 ,且
,且 ,其中
,其中
(1)求数列 的通项公式;
的通项公式;
(2)若 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
(1) ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)利用 ,表示出数列的通项,再由已知求出
,表示出数列的通项,再由已知求出 ,整理得到
,整理得到 ,
,
利用“累积法”,则 ,即
,即 ,得
,得
验证 时也符合即可;
时也符合即可;
(2)由(1)得 ,根据裂项相消法,将
,根据裂项相消法,将 拆为
拆为 ,将
,将 拆为
拆为 ,则
,则 ,
,
 将上式中消去相同的项进行整理即可证得.
将上式中消去相同的项进行整理即可证得.
试题解析:(1)令 ,得
,得 ,即
,即 ,由已知
,由已知 ,得
,得 1分
1分
把式子 中的
中的 用
用 替代,得到
替代,得到
由 可得
可得
即 ,即
,即
即得: , 3分
, 3分
所以:
即  6分
6分
又 ,所以
,所以
又 ,
, 8分
8分
(2)由(1)知
又
 11分
11分

 14分
14分
考点:1、用 表示
表示 ;2、不等式的性质;3、累积法、裂项相消法.
;2、不等式的性质;3、累积法、裂项相消法.

练习册系列答案
相关题目
 为纯虚数,若
为纯虚数,若 (
( 为虚数单位),则实数
为虚数单位),则实数 的值为 .
的值为 . 的展开式中,记
的展开式中,记 项的系数为f(
项的系数为f( ,
, ),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .
),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .  .若
.若 是偶函数,则
是偶函数,则 .
.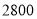 人,其中高一年级
人,其中高一年级 人,高二年级
人,高二年级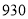 人,高三年级
人,高三年级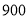 人,现采用分层抽样的方法,抽取
人,现采用分层抽样的方法,抽取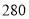 人进行体育达标检测,则抽取高二年级学生人数为 .
人进行体育达标检测,则抽取高二年级学生人数为 . 与
与 相交于点
相交于点 、
、 两点,则
两点,则 ______.
______. 为等比数列{
为等比数列{ }的前n项和,
}的前n项和, =0,则
=0,则 =( ).
=( ). 的前
的前 项和记为
项和记为 ,且
,且 ,
, ,则
,则 .
.  ,若
,若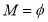 ,则实数
,则实数 的取值范围是_______________ .
的取值范围是_______________ .