题目内容
设等差数列 的前
的前 项和为
项和为 且
且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ,并求
,并求 的最小值.
的最小值.
 的前
的前 项和为
项和为 且
且 .
.(1)求数列
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和 ,并求
,并求 的最小值.
的最小值.(1)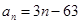 ;(2)当
;(2)当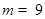 或
或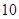 时,
时, 最小,最小值为
最小,最小值为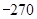 .
.
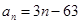 ;(2)当
;(2)当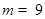 或
或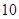 时,
时, 最小,最小值为
最小,最小值为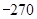 .
.试题分析:(1)设等差数列
 的公差为
的公差为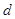 ,进而根据条件列出方程组
,进而根据条件列出方程组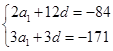 ,从中求解得到
,从中求解得到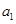 与
与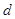 ,进而可以写出数列
,进而可以写出数列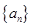 的通项公式;(2)由(1)中结论可得
的通项公式;(2)由(1)中结论可得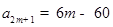 ,法一:进而根据等差数列的通项公式求出该数列的前
,法一:进而根据等差数列的通项公式求出该数列的前 项和
项和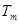 ,再由二次函数的图像与性质即可求得
,再由二次函数的图像与性质即可求得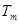 的最小值;法二:也可以由
的最小值;法二:也可以由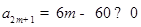 得出该数列从首项开始到哪一项都是非正常,所有这些非正数相加,当然是达到
得出该数列从首项开始到哪一项都是非正常,所有这些非正数相加,当然是达到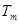 的最小值.
的最小值.(1)设等差数列
 的公差为
的公差为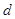 ,由已知可得
,由已知可得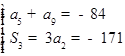 即
即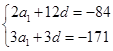 ,解得
,解得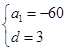 ,所以
,所以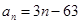
(2)法一:由(1)可得
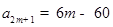 ,则由等差数列的前
,则由等差数列的前 项和公式可得
项和公式可得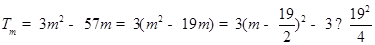
因为
 为整数,根据二次函数的图像与性质可知:当
为整数,根据二次函数的图像与性质可知:当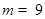 或
或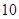 时,
时, 最小,最小值为
最小,最小值为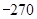
法二:由(1)可得
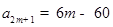 ,所以该数列是单调递增数列,令
,所以该数列是单调递增数列,令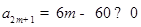 ,解得
,解得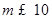 所以当
所以当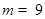 或
或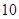 时,
时, 最小,最小值为
最小,最小值为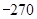 .
. 项和;2.二次函数的图像与性质.
项和;2.二次函数的图像与性质.
练习册系列答案
相关题目
 满足:
满足: 且
且 .
. ,数列
,数列 的前项和为
的前项和为 ,求证:
,求证: 时,
时, 且
且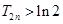
 满足
满足 ,
, ,数列
,数列 满足
满足 .
. ,求满足不等式
,求满足不等式 的所有正整数
的所有正整数 的值.
的值. 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项 ,
, 、
、 、…、
、…、 恰为等比数列,且
恰为等比数列,且 ,
, ,
, .
. (用
(用 表示);
表示); 的前
的前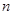 项和为
项和为 ,求
,求 所表示的平面区域为
所表示的平面区域为 ,记
,记
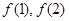 的值及
的值及 的表达式;
的表达式; 为数列
为数列 的前
的前 项的和,其中
项的和,其中 ,问是否存在正整数
,问是否存在正整数 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数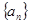 满足
满足 (
( 为常数),则称数列
为常数),则称数列 ,
, ,则
,则 ( )
( ) 

 ,则
,则 ( )
( )



 为等差数列
为等差数列 的前
的前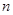 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则 ( )
( )


