Question

设函数f（x）=|x²-2x-8|．
（1）在区间[-3，5]上画出函数f（x）的图象；
（2）设集合A={x|f（x）≥5}，B=（-∞，-3]∪[-1，3]∪[5，+∞）．写出集合A和B之间的关系（相等或子集或真子集）；
（3）当k＞2时，求证：在区间[-2，4]上，函数f（x）图象位于函数y=kx+4k的图象的下方．

Answer 1

分析：（1）根据函数的解析式作出函数的图象即可．
（2）求出集合A，利用两个集合元素之间的关系确定集合关系．
（3）将图象关系转化为对应的不等式g（x）=k（x+4）-（-x²+2x+8）＜0，然后证明即可．

解答：解：（1）如图…（4分）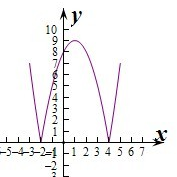
（2）方程f （x）=5的解分别是1-

14

，-1，3和1+

14

，
由于f（x）在（-∞，-2]和[1，4]上单调递减，在[-2，1]和[4，+∞）上单调递增，因此
A=(-∞，1-

14

]∪[-1，3]∪[1+

14

，+∞)．…（6分）
由于1+

14

＜5，1-

14

＞-3，
∴B?A…（8分）
（3）在区间[-2，4]上，函数f（x）图象位于函数y=kx+4k的图象的下方．
则只要证明g（x）=k（x+4）-（-x²+2x+8）＜0即可．
当x∈[-2，4]时，f（x）=-x²+2x+8．
g（x）=k（x+4）-（-x²+2x+8）=x2+(k-2)x+(4k-8)=(x-

2-k

2

)2-

k2-20k+36

4

，
∵k＞2，∴

2-k

2

＜0．又-2≤x≤6，…（10分）
①当-2≤

2-k

2

＜0，即2＜k≤6时，取x=

2-k

2

，g(x)min=-

k2-20k+36

4

=-

1

4

[(k-10)2-64]．
∵16≤（k-10）²＜64，∴（k-10）²-64＜0，
则g（x）_min＞0．…（12分）
②当

2-k

2

＜-2， 即k＞6 时， 取x=-2，g(x)min=2k＞0．
由①、②可知，当k＞2时，g （x）＞0，x∈[-2，4]．
因此，在区间[-2，4]上，函数f （x）图象位于y=k（x+4）的图象的下方．…（14分）

点评：本题主要考查二次函数图象和性质的应用，综合性较强，运算量较大．