题目内容
已知函数f(x)=x2-cosx,对于[- ,
, ]上的任意x1,x2,有如下条件:
]上的任意x1,x2,有如下条件:①x1>x2;②x12>x22;③|x1|>x2.
其中能使f(x1)>f(x2)恒成立的条件序号是 .
【答案】分析:先研究函数的性质,观察知函数是个偶函数,由于f′(x)=2x+sinx,在[0,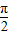 ]上f′(x)>0,可推断出函数在y轴两边是左减右增,此类函数的特点是自变量离原点的位置越近,则函数值越小,欲使f(x1)>f(x2)恒成立,只需x1,到原点的距离比x2,到原点的距离大即可,由此可得出|x1|>|x2|,在所给三个条件中找符合条件的即可.
]上f′(x)>0,可推断出函数在y轴两边是左减右增,此类函数的特点是自变量离原点的位置越近,则函数值越小,欲使f(x1)>f(x2)恒成立,只需x1,到原点的距离比x2,到原点的距离大即可,由此可得出|x1|>|x2|,在所给三个条件中找符合条件的即可.
解答:解:函数f(x)为偶函数,f′(x)=2x+sinx,
当0<x≤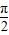 时,0<sinx≤1,0<2x≤π,
时,0<sinx≤1,0<2x≤π,
∴f′(x)>0,函数f(x)在[0,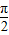 ]上为单调增函数,
]上为单调增函数,
由偶函数性质知函数在[-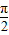 ,0]上为减函数.
,0]上为减函数.
当x12>x22时,得|x1|>|x2|≥0,
∴f(|x1|)>f(|x2|),由函数f(x)在上[-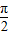 ,
,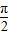 ]为偶函数得f(x1)>f(x2),故②成立.
]为偶函数得f(x1)>f(x2),故②成立.
∵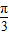 >-
>-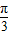 ,而f(
,而f(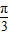 )=f(
)=f(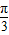 ),
),
∴①不成立,同理可知③不成立.故答案是②.
故应填②
点评:本题考查函数的性质奇偶性与单调性,属于利用性质推导出自变量的大小的问题,本题的解题方法新颖,判断灵活,方法巧妙.
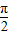 ]上f′(x)>0,可推断出函数在y轴两边是左减右增,此类函数的特点是自变量离原点的位置越近,则函数值越小,欲使f(x1)>f(x2)恒成立,只需x1,到原点的距离比x2,到原点的距离大即可,由此可得出|x1|>|x2|,在所给三个条件中找符合条件的即可.
]上f′(x)>0,可推断出函数在y轴两边是左减右增,此类函数的特点是自变量离原点的位置越近,则函数值越小,欲使f(x1)>f(x2)恒成立,只需x1,到原点的距离比x2,到原点的距离大即可,由此可得出|x1|>|x2|,在所给三个条件中找符合条件的即可.解答:解:函数f(x)为偶函数,f′(x)=2x+sinx,
当0<x≤
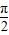 时,0<sinx≤1,0<2x≤π,
时,0<sinx≤1,0<2x≤π,∴f′(x)>0,函数f(x)在[0,
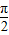 ]上为单调增函数,
]上为单调增函数,由偶函数性质知函数在[-
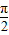 ,0]上为减函数.
,0]上为减函数.当x12>x22时,得|x1|>|x2|≥0,
∴f(|x1|)>f(|x2|),由函数f(x)在上[-
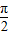 ,
,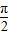 ]为偶函数得f(x1)>f(x2),故②成立.
]为偶函数得f(x1)>f(x2),故②成立.∵
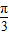 >-
>-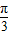 ,而f(
,而f(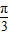 )=f(
)=f(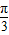 ),
),∴①不成立,同理可知③不成立.故答案是②.
故应填②
点评:本题考查函数的性质奇偶性与单调性,属于利用性质推导出自变量的大小的问题,本题的解题方法新颖,判断灵活,方法巧妙.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|