题目内容
已知:sin(
-x)=
,且
π<x<
π,求
的值.
| π |
| 4 |
| 3 |
| 5 |
| 17 |
| 12 |
| 7 |
| 4 |
| sin2x+2sin2x |
| 1-tanx |
分析:利用同角三角函数的基本关系求出cos(
-x),由两角差的正切公式求得tanx,利用二倍角公式求出sin2x 和sin2x 的值,
从而求得
的值.
| π |
| 4 |
从而求得
| sin2x+2sin2x |
| 1-tanx |
解答:解:∵
π<x<
π,∴-
π<
-x<-
π,
∴cos(
-x)=-
,tan(
-x)=-
,即-
=
∴tanx=7,
sin2x=sin[
-2(
-x)]=cos2(
-x)=2cos2(
-x)-1=
,sin2x=
=
-
sin2(
-x)=
-sin(
-x)cos(
-x)=
,
∴
=
=-
.
| 17 |
| 12 |
| 7 |
| 4 |
| 3 |
| 2 |
| π |
| 4 |
| 7 |
| 6 |
∴cos(
| π |
| 4 |
| 4 |
| 5 |
| π |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1-tanx |
| 1+tanx |
sin2x=sin[
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 7 |
| 25 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 37 |
| 50 |
∴
| sin2x+2sin2x |
| 1-tanx |
| ||||
| 1-7 |
| 22 |
| 3 |
点评:本题考查两角和差的正切,同角三角函数的基本关系,二倍角公式的应用,角的变换是解题的难点和关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 =
= tan
tan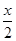 -
-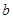 sin
sin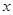 +4(其中
+4(其中
 0),如果
0),如果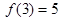 ,则
,则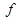 (2010
(2010 -3)的值为 ( )
-3)的值为 ( )