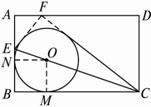
题目内容
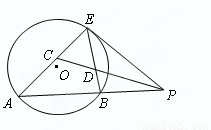
如图,已知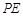 切⊙
切⊙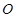 于点E,割线PBA交⊙
于点E,割线PBA交⊙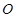 于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.求证:
于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.求证:
(Ⅰ)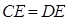 ;
;
【答案】
(Ⅰ)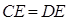 ;
(Ⅱ)
;
(Ⅱ)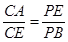 .
.
【解析】
试题分析:(Ⅰ)要证两边相等,只需证明角相等,根据圆中切线与割线的关系进行转化,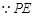 切⊙
切⊙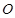 于点
于点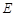 ,
,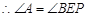 ,
,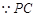 平分
平分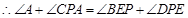
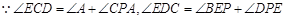 ,
, 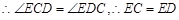 .(2)证明边长成比例,需要证明两个三角形相似,
.(2)证明边长成比例,需要证明两个三角形相似,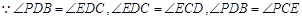
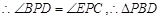 ∽
∽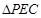 ,
,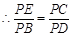 同理
同理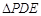 ∽
∽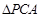 ,
,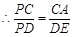
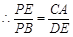
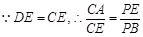
试题解析:(Ⅰ)证明: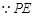 切⊙
切⊙ 于点
于点 ,
,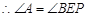
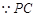 平分
平分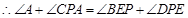
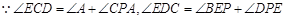 ,
,
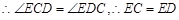
(Ⅱ)证明: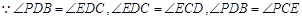
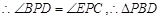 ∽
∽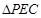 ,
,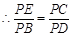
同理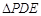 ∽
∽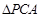 ,
,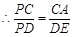
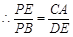
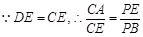
考点:1.简单的几何证明.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
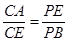 .
. (2013•许昌二模)如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE、BE分别交于点C,D
(2013•许昌二模)如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE、BE分别交于点C,D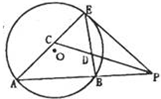 (2012•洛阳模拟)选修4-1:几何证明选讲
(2012•洛阳模拟)选修4-1:几何证明选讲 切⊙
切⊙ 于点E,割线PBA交⊙
于点E,割线PBA交⊙
 ;
; .
. 切⊙
切⊙ 于点E,割线PBA交⊙
于点E,割线PBA交⊙
 ;
; .
.