题目内容
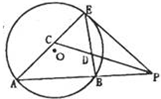
（2012•洛阳模拟）选修4-1：几何证明选讲如图，已知PE切⊙O于点E，割线PBA交⊙O于A，B两点，∠APE的平分线和AE，BE分别交于点C，D．
求证：（1）CE=DE；
（2）
| CA |
| CE |
| PE |
| PB |
分析：（1）由弦切角定理是，及PC为∠APE的平分线，可证得∠ECD=∠EDC，进而证得CE=DE
（2）先由AA证明出△PBC∽△ECD，进而证得△PBC∽△PEC，可由相似三角形对应边成比例得到结论．
（2）先由AA证明出△PBC∽△ECD，进而证得△PBC∽△PEC，可由相似三角形对应边成比例得到结论．
解答：解：（1）PE切圆O于点E
∴∠A=∠BEP
∵PC平分∠APE，
∴∠A+∠CPA=∠BEP+∠DPE
∵∠ECD=∠A+∠CPA，∠EDC=∠BEP+∠DPE
∴∠ECD=∠EDC，
∴EC=ED
（2）∵∠PDB=∠EDC，∠EDC=∠ECD
∴∠PDB=∠PCE
∵∠BPD=∠EPC
∴△PDB∽△PEC
∴
=
同理△PDE∽△PCA
∴
=
∴
=
∵DE=CE
∴
=
∴∠A=∠BEP
∵PC平分∠APE，
∴∠A+∠CPA=∠BEP+∠DPE
∵∠ECD=∠A+∠CPA，∠EDC=∠BEP+∠DPE
∴∠ECD=∠EDC，
∴EC=ED
（2）∵∠PDB=∠EDC，∠EDC=∠ECD
∴∠PDB=∠PCE
∵∠BPD=∠EPC
∴△PDB∽△PEC
∴
| PE |
| PB |
| PC |
| PD |
同理△PDE∽△PCA
∴
| PC |
| PD |
| CA |
| DE |
∴
| PE |
| PB |
| CA |
| DE |
∵DE=CE
∴
| CA |
| CE |
| PE |
| PB |
点评：本题考查的往右点是与圆相关的比例线段，相似三角形的性质，熟练掌握弦切角定理及相似三角形的判定及性质是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
（2012•洛阳模拟）阅读如图的算法框图，输出的结果S的值为（ ）