题目内容
(12分)设函数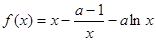
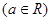 .
.
(I)若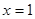 是函数
是函数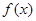 的极大值点,求
的极大值点,求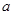 的取值范围;
的取值范围;
(II)当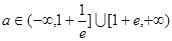 时,若在
时,若在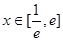 上至少存在一点
上至少存在一点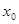 ,使
,使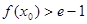 成立,求
成立,求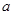 的取值范围.
的取值范围.
【答案】
(I)当 ,即
,即 时,
时, 是函数
是函数 的极大值点.
的极大值点.
(II)当 时,在
时,在 上至少存在一点
上至少存在一点 ,使
,使 .
.
【解析】解: …1分
…1分
|
|
|
|
|
|
|
|
|
|
|
|
递减 |
极小值 |
递增 |
当 时,
时,
当 时,
时,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
递增 |
极大值 |
递减 |
极小值 |
递增 |
|
|
|
|
|
|
|
|
|
|
|
|
递增 |
非极值 |
递增 |
当 时,
时,
当 时,
时,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
递增 |
极大值 |
递减 |
极小值 |
递增 |
综上所述,当 ,即
,即 时,
时, 是函数
是函数 的极大值点.………………6分
的极大值点.………………6分
(2)问题等价于当 时,
时, .………………7分
.………………7分
由(1)知,①当 ,即
,即 时,函数
时,函数 在
在 上递减,在
上递减,在 上递增,
上递增, .由
.由 ,解得
,解得 .由
.由 ,解得
,解得
 ,
, ;………………9分
;………………9分
②当 ,即
,即 时,函数
时,函数 在
在 上递增,在
上递增,在 上递减,
上递减,
 .………………11分
.………………11分
综上所述,当 时,在
时,在 上至少存在一点
上至少存在一点 ,使
,使 成立…12分
成立…12分

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目












 。若
。若 是奇函数,则
是奇函数,则 _________.
_________.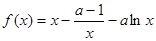
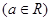 .
.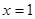 是函数
是函数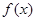 的极大值点,求
的极大值点,求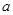 的取值范围;
的取值范围;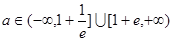 时,若在
时,若在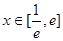 上至少存在一点
上至少存在一点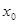 ,使
,使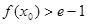 成立,求
成立,求
 .
. 是函数
是函数 的极大值点,求
的极大值点,求 的取值范围;
的取值范围; 时,若在
时,若在 上至少存在一点
上至少存在一点 ,使
,使 成立,求
成立,求