题目内容
 如图所示,在斜三棱柱ABC-A1B1C1中,∠A1AC=∠ACB=
如图所示,在斜三棱柱ABC-A1B1C1中,∠A1AC=∠ACB=| π |
| 2 |
| π |
| 6 |
与底面所成的角为
| π |
| 3 |
| 3 |
分析:如图,在Rt△AA1C中求出AC,作B1H⊥平面ABC,垂足为H,则∠B1BH=
,求出B1H就是棱柱的高,然后求出斜三棱柱ABC-A1B1C1的体积.
| π |
| 3 |
解答: 解:在Rt△AA1C中,AC=AA1•tan∠AA1C=4
解:在Rt△AA1C中,AC=AA1•tan∠AA1C=4
×
=4.
作B1H⊥平面ABC,垂足为H,则∠B1BH=
,
在Rt△B1BH中,B1H=BB1•sin∠B1BH=AA1•sin
=4
×
=6.
∴V=S△ABC•B1H=
×4×4×6=48.
 解:在Rt△AA1C中,AC=AA1•tan∠AA1C=4
解:在Rt△AA1C中,AC=AA1•tan∠AA1C=4| 3 |
| ||
| 3 |
作B1H⊥平面ABC,垂足为H,则∠B1BH=
| π |
| 3 |
在Rt△B1BH中,B1H=BB1•sin∠B1BH=AA1•sin
| π |
| 3 |
| 3 |
| ||
| 2 |
∴V=S△ABC•B1H=
| 1 |
| 2 |
点评:本题是基础题,考查斜三棱柱ABC-A1B1C1的体积的求法,求出底面面积,它的高是本题的难点,注意正确分析,仔细体会.

练习册系列答案
相关题目
如图所示,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在面ABC上的射影H必在( )
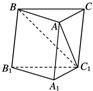

| A、直线AB上 | B、直线BC上 | C、直线CA上 | D、△ABC内部 |
 7、如图所示,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在直线
7、如图所示,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在直线
