题目内容
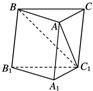
如图所示，在斜三棱柱A1B1C1—ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC.
（1）若D是BC的中点.求证：AD⊥CC1；
（2）过侧面BB1C1C的对角线BC1的平面交侧棱于M，若AM=MA1，
求证：截面MBC1⊥侧面BB1C1C.
证明略
解析:
（1）∵AB=AC，D是BC的中点，∴AD⊥BC.
∵平面ABC⊥平面BB1C1C，交线为BC.
∴由面面垂直的性质定理，
可知AD⊥平面BB1C1C.
又∵CC1
平面BB1C1C，
∴AD⊥CC1.
（2）取BC1的中点E，连接DE、ME.
在△BCC1中，D、E分别是BC、BC1的中点，
∴DE
CC1.又AA1 CC1，∴DEAA1.
∵M是AA1的中点（由AM=MA1知），∴DEAM.
∴四边形AMED是平行四边形，∴ADME.
由（1）知AD⊥平面BB1C1C.
∴ME⊥平面BB1C1C.
又∵ME平面BMC1，
∴平面BMC1⊥平面BB1C1C.
练习册系列答案
相关题目
如图所示，在斜三棱柱ABC-A1B1C1中，∠BAC=90°，BC1⊥AC，则C1在面ABC上的射影H必在（ ）
| A、直线AB上 | B、直线BC上 | C、直线CA上 | D、△ABC内部 |
7、如图所示，在斜三棱柱ABC-A1B1C1中，∠BAC=90°，BC1⊥AC，则C1在底面ABC上的射影H必在直线
如图所示，在斜三棱柱ABC-A1B1C1中，∠A1AC=∠ACB=