题目内容
四棱锥P-ABCD底面为正方形，侧面PAD为等边三角形，且侧面PAD⊥底面ABCD，点M在底面正方形ABCD内运动，且满足MP=MC，则点M在正方形ABCD内的轨迹一定是
- A.
- B.
- C.
- D.
B
分析：先确定轨迹是2个平面的交线，PC的中垂面α和正方形ABCD的交线，再确定交线的准确位置，即找到交线上的2个固定点．
解答：∵MP=MC，
∴M在PC的中垂面α上，点M在正方形ABCD内的轨迹一定是平面α和正方形ABCD的交线，
∵ABCD为正方形，侧面PAD为等边三角形，
∴PD=CD，取PC的中点N，有DN⊥PC，
取AB中点H，可证 CH=HP，
∴HN⊥PC，
∴点M在正方形ABCD内的轨迹一定是HD．
故答案选 B．
点评：本题考查面面垂直的性质，轨迹的确定方法．
分析：先确定轨迹是2个平面的交线，PC的中垂面α和正方形ABCD的交线，再确定交线的准确位置，即找到交线上的2个固定点．
解答：∵MP=MC，
∴M在PC的中垂面α上，点M在正方形ABCD内的轨迹一定是平面α和正方形ABCD的交线，
∵ABCD为正方形，侧面PAD为等边三角形，
∴PD=CD，取PC的中点N，有DN⊥PC，
取AB中点H，可证 CH=HP，
∴HN⊥PC，
∴点M在正方形ABCD内的轨迹一定是HD．
故答案选 B．
点评：本题考查面面垂直的性质，轨迹的确定方法．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
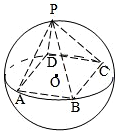如图，正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上，点P在球面上，若
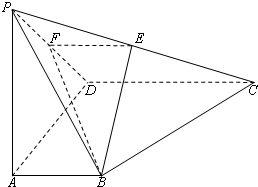如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AB，CD⊥DA，CD=2AB，PA⊥底面ABCD，E、F分别为PC，PD的中点，PA=AD=AB．
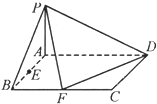已知四棱锥P-ABCD底面ABCD是矩形，PA丄平面ABCD，AD=4，AB=2，E，F分别是线段AB和BC的中点．
如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，PA⊥底面ABCD，E为PC的中点，PA=AD=AB=1．
（2008•上海一模）如图，正四棱锥P-ABCD底面的四个顶点A，B，C，D在球O的同一个大圆上，点P在球面上，且已知