题目内容
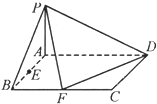已知四棱锥P-ABCD底面ABCD是矩形，PA丄平面ABCD，AD=4，AB=2，E，F分别是线段AB和BC的中点．（1）证明：DF⊥平面PAF
（2）在线段AP上找一点G，使得EG∥平面PFD．
分析：（1）证明AF⊥DF，利用PA丄平面ABCD，可得PA⊥DF，利用线面垂直的判定定理，即可得出结论；
（2）过点E作EH∥FD，交AD于点H，则EH∥平面PFD，且AH=
AD，再过点H作HG∥DP交PA于点G，则HG∥平面PFD且AG=
AP，从而平面GEH∥平面PFD，即可得出结论．
（2）过点E作EH∥FD，交AD于点H，则EH∥平面PFD，且AH=
| 1 |
| 4 |
| 1 |
| 4 |
解答：
（1）证明：连接AF，则AF=2
，DF=2
，
∵AD=4
∴AF2+DF2=AD2
∴AF⊥DF…（3分）
∵PA丄平面ABCD，
∴PA⊥DF，
∵PA∩AF=A
∴DF⊥平面PAF…（6分）
（2）解：过点E作EH∥FD，交AD于点H，则EH∥平面PFD，且AH=
AD．
再过点H作HG∥DP交PA于点G，则HG∥平面
PFD且AG=
AP，
∴平面GEH∥平面PFD．…（10分）
∵EG?平面GEH，∴EG∥平面PFD．
从而满足AG=
AP的点G为所求．…（12分）
（1）证明：连接AF，则AF=2| 2 |
| 2 |
∵AD=4
∴AF2+DF2=AD2
∴AF⊥DF…（3分）
∵PA丄平面ABCD，
∴PA⊥DF，
∵PA∩AF=A
∴DF⊥平面PAF…（6分）
（2）解：过点E作EH∥FD，交AD于点H，则EH∥平面PFD，且AH=
| 1 |
| 4 |
再过点H作HG∥DP交PA于点G，则HG∥平面
PFD且AG=| 1 |
| 4 |
∴平面GEH∥平面PFD．…（10分）
∵EG?平面GEH，∴EG∥平面PFD．
从而满足AG=
| 1 |
| 4 |
点评：本题考查线面垂直，线面平行，考查学生分析解决问题的能力，正确运用线面垂直，线面平行的判定定理是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．