题目内容
已知圆x2+(y-1)2=2上任一点P(x,y),其坐标均使得不等式x+y+m≥0恒成立,则实数m的取值范围是
- A.[1,+∞)
- B.(-∞,1]
- C.[-3,+∞)
- D.(-∞,-3]
A
分析:把已知的不等式恒成立即m≥-x-y恒成立,即m要大于等于-x-y的最大值,求-x-y的最大值的方法是:因为P为圆上的一点,所以P的坐标满足圆的方程,给圆的方程两边除以2后,利用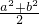 ≥
≥ 即可得到x+y-1的范围,然后求出-x-y的范围即可得到-x-y的最大值,令m大于等于这个最大值,即可得到满足题意的m的范围.
即可得到x+y-1的范围,然后求出-x-y的范围即可得到-x-y的最大值,令m大于等于这个最大值,即可得到满足题意的m的范围.
解答:∵x+y+m≥0,即m≥-x-y恒成立,∴只须求出-x-y的最大值即可,
∵1= ≥
≥ ,
,
∴(x+y-1)2≤4,解得-2≤x+y-1≤2,即-1≤x+y≤3,
∴-3≤-x-y≤1,
∴-x-y的最大值是1,
则m≥1,所以实数m的取值范围是[1,+∞).
故选A
点评:此题考查学生掌握不等式恒成立时所满足的条件,会利用基本不等式求函数的最值,是一道综合题.
分析:把已知的不等式恒成立即m≥-x-y恒成立,即m要大于等于-x-y的最大值,求-x-y的最大值的方法是:因为P为圆上的一点,所以P的坐标满足圆的方程,给圆的方程两边除以2后,利用
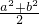 ≥
≥ 即可得到x+y-1的范围,然后求出-x-y的范围即可得到-x-y的最大值,令m大于等于这个最大值,即可得到满足题意的m的范围.
即可得到x+y-1的范围,然后求出-x-y的范围即可得到-x-y的最大值,令m大于等于这个最大值,即可得到满足题意的m的范围.解答:∵x+y+m≥0,即m≥-x-y恒成立,∴只须求出-x-y的最大值即可,
∵1=
 ≥
≥ ,
,∴(x+y-1)2≤4,解得-2≤x+y-1≤2,即-1≤x+y≤3,
∴-3≤-x-y≤1,
∴-x-y的最大值是1,
则m≥1,所以实数m的取值范围是[1,+∞).
故选A
点评:此题考查学生掌握不等式恒成立时所满足的条件,会利用基本不等式求函数的最值,是一道综合题.

练习册系列答案
相关题目
已知圆x2+(y-1)2=2上任一点P(x,y),其坐标均使得不等式x+y+m≥0恒成立,则实数m的取值范围是( )
| A、[1,+∞) | B、(-∞,1] | C、[-3,+∞) | D、(-∞,-3] |
已知圆x2+(y-1)2=1上任意一点P(x,y)都使不等式x+y+m≥0成立,则m的取值范围是( )
A、[
| ||
| B、(-∞,0] | ||
C、(
| ||
D、[1-
|