题目内容
1.已知$a={log_3}\sqrt{2}$,$b={log_{\frac{1}{3}}}2$,$c={2^{\frac{1}{3}}}$,则a,b,c的大小关系是( )| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
分析 由已知条件利用对数函数和指数函数的单调性求解.
解答 解:∵1=log33>$a={log_3}\sqrt{2}$>$b={log_{\frac{1}{3}}}2$=$lo{g}_{3}\frac{1}{2}$,$c={2^{\frac{1}{3}}}$>20=1,
∴b<a<c.
故选:B.
点评 本题考查三个数的大小的求法,是基础题,解题时要认真审题,注意对数函数、指数函数的性质的合理运用.

练习册系列答案
相关题目
12.已知全集U=R,集合M={x|x2-2x<0},集合N={x|x>1},则集合M∩(∁UN)=( )
| A. | {x|0<x<1} | B. | {x|0<x≤1} | C. | {x|0<x<2} | D. | {x|x≤1} |
16.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≥3}\\{f(x+1),x<3}\end{array}\right.$,则f(1+log23)的值为( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
11.若点A、B、C、D均在平面α内,点P不在平面α内,则“点P、A、B、C、D在同一球面上”是“A、B、C、D四点共圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
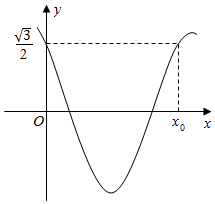 已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.