题目内容
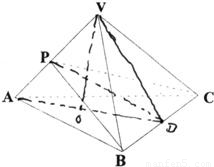
 如图,正三棱锥V-ABC的底面边长为a,侧棱与底面所成的角等于θ,过底面一边作棱锥的截面,当截面与底面所成二面角为何值时,截面面积最小?并求出最小值.
如图,正三棱锥V-ABC的底面边长为a,侧棱与底面所成的角等于θ,过底面一边作棱锥的截面,当截面与底面所成二面角为何值时,截面面积最小?并求出最小值.分析:作VO⊥平面ABC,由正三棱锥的几何特征可得O为△ABC的中心,连接AO并延长交BC于D,则∠DAO=θ,连接VD,PD,由线面垂直及面面垂直的判定定理可得BC⊥平面VAD,进而PDC平面VAD,∠PDA为截面与底面所成角,根据正弦定理我们可以得到PD长的表达式,根据正弦函数的性质求出PD的最小值,即可得到答案.
解答:解:作VO⊥平面ABC,O为垂足,因为V-ABC是正三棱锥,所以O为△ABC的中心,
连接AO并延长交BC于D,则AD⊥BC,∠DAO=θ
连接VD,PD
∴BC⊥VA∴BC⊥平面VAD,进而PDC平面VAD…(4分)
∴PD⊥BC∴∠PDA为截面与底面所成角,设为x,在△PAD中,∠PAD=θ,∠PDA=x,∴∠APD=180°-(θ+π) …(4分)
根据正弦定理得
=
PD=
=
≥
asinθ(4分)
当且仅当sin(θ+x)=1,θ+x=90°,x=90°-θ的等号成立,∴PD最小
∴S△PBC最小面积=
a•
asinθ=
a2sinθ
连接AO并延长交BC于D,则AD⊥BC,∠DAO=θ
连接VD,PD
∴BC⊥VA∴BC⊥平面VAD,进而PDC平面VAD…(4分)
∴PD⊥BC∴∠PDA为截面与底面所成角,设为x,在△PAD中,∠PAD=θ,∠PDA=x,∴∠APD=180°-(θ+π) …(4分)
根据正弦定理得
| PD |
| sinθ |
| AD |
| sin[180°-(θ+x)] |
| ||||
| sin(θ+x) |
| ||
| 2sin(θ+x) |
| ||
| 2 |
当且仅当sin(θ+x)=1,θ+x=90°,x=90°-θ的等号成立,∴PD最小
∴S△PBC最小面积=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:本题考查的点是与二面角有关的立体几何问题,其中根据正弦定理得到PD长的表达式,进而根据正弦函数的性质求出PD的最小值,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
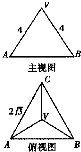 如图是正三棱锥V-ABC的主视图,俯视图,根据图中尺寸,则该三棱锥的侧视图面积为( )
如图是正三棱锥V-ABC的主视图,俯视图,根据图中尺寸,则该三棱锥的侧视图面积为( )| A、9 | ||||
| B、6 | ||||
C、
| ||||
D、
|
 已知正三棱锥V-ABC的侧棱长为4,底边长为
已知正三棱锥V-ABC的侧棱长为4,底边长为