题目内容
已知锐角α,β满足sinα=
,cosβ=
,则α+β=
.
| ||
| 5 |
3
| ||
| 10 |
| π |
| 4 |
| π |
| 4 |
分析:由α、β∈(0,
),利用同角三角函数的关系算出cosα、sinβ的值,进而根据两角和的余弦公式算出cos(α+β)=
,结合α+β∈(0,π)可得α+β的值.
| π |
| 2 |
| ||
| 2 |
解答:解:∵α、β∈(0,
),满足sinα=
,cosβ=
,
∴cosα=
=
,sinβ=
=
.
由此可得cos(α+β)=cosαcosβ-sinαsinβ=
•
-
•
=
.
又∵α+β∈(0,π),∴α+β=
.
故答案为:
| π |
| 2 |
| ||
| 5 |
3
| ||
| 10 |
∴cosα=
| 1-sin2α |
2
| ||
| 5 |
| 1-cos 2β |
| ||
| 10 |
由此可得cos(α+β)=cosαcosβ-sinαsinβ=
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 5 |
| ||
| 2 |
又∵α+β∈(0,π),∴α+β=
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题给出角α、β满足的条件,求α+β的值.着重考查了特殊角的三角函数值、同角三角函数的基本关系、两角和的余弦公式等知识,属于中档题.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: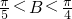 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);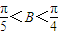 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);