题目内容
(文)已知锐角三角形ABC的三边为连续整数,且角A、B满足A=2B.
(1)当
<B<
时,求△ABC的三边长及角B(用反三角函数值表示);
(2)求△ABC的面积S.
(1)当
| π |
| 5 |
| π |
| 4 |
(2)求△ABC的面积S.
(1)设△ABC的三边为n-1,n,n+1(n≥3,n∈N),
由题设A=2B得:C=π-A-B=π-3B,
由题意
<B<
,得
<A<
,
可得
<C<
,
从而A>C>B,得角B所对的边为n-1,角A所对的边为n+1,(4分)
故有
=
,
得cosB=
,又cosB=
,
得
=
,
解得n=5,
故△ABC的三边长为4,5,6,(7分)
得cosB=
,从而B=arccos
;(10分)
(2)由B=arccos
,得到cosB=
,又B为锐角,
∴sinB=
,又a=6,c=5,
则S=
acsinB=
.(14分)
由题设A=2B得:C=π-A-B=π-3B,
由题意
| π |
| 5 |
| π |
| 4 |
| 2π |
| 5 |
| π |
| 2 |
可得
| π |
| 4 |
| 2π |
| 5 |
从而A>C>B,得角B所对的边为n-1,角A所对的边为n+1,(4分)
故有
| n-1 |
| sinB |
| n+1 |
| sin2B |
得cosB=
| n+1 |
| 2(n-1) |
| n2+(n+1)2-(n-1)2 |
| 2n(n+1) |
得
| n+1 |
| 2(n-1) |
| n2+(n+1)2-(n-1)2 |
| 2n(n+1) |
解得n=5,
故△ABC的三边长为4,5,6,(7分)
得cosB=
| 3 |
| 4 |
| 3 |
| 4 |
(2)由B=arccos
| 3 |
| 4 |
| 3 |
| 4 |
∴sinB=
| ||
| 4 |
则S=
| 1 |
| 2 |
15
| ||
| 4 |

练习册系列答案
相关题目
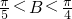 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);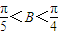 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);