题目内容
正方体ABCD-A′B′C′D′中，E为DD′的中点，则BD′与平面ACE的位置关系是 ．
【答案】分析：连接BD′，AC，BD，设AC，BD交于点O，连接OE，由正方体ABCD-A′B′C′D′中，E为DD′的中点，知OE∥BD′，由此能够推导出BD′∥平面ACE．
解答：
解：连接BD′，AC，BD，设AC，BD交于点O，连接OE，
∵正方体ABCD-A′B′C′D′中，E为DD′的中点，
∴OE∥BD′，
∵OE?面ACE，BD′?面ACE，
∴BD′∥平面ACE．
故答案为：平行．
点评：本题考查空间中直线与平面之间的位置关系，是基础题．解题时要认真审题，注意直线与平面平行的判定定理的合理运用．
解答：
解：连接BD′，AC，BD，设AC，BD交于点O，连接OE，∵正方体ABCD-A′B′C′D′中，E为DD′的中点，
∴OE∥BD′，
∵OE?面ACE，BD′?面ACE，
∴BD′∥平面ACE．
故答案为：平行．
点评：本题考查空间中直线与平面之间的位置关系，是基础题．解题时要认真审题，注意直线与平面平行的判定定理的合理运用．
练习册系列答案
相关题目
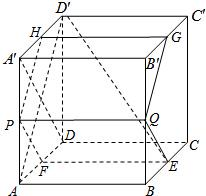如图，在棱长为1的正方体ABCD-A′B′C′D′中，AP=BQ=b（0＜b＜1），截面PQEF∥A′D，截面PQGH∥AD′．
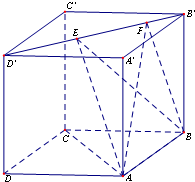如图，正方体ABCD-A′B′C′D′的棱长为1，线段B′D′上有两个动点E，F且
（2011•蓝山县模拟）如图，在正方体ABCD-A′B′C′D′中，异面直线BD与B′C所成角为