题目内容
已知函数f(x)对任意x∈R满足f(x+1)=f(x-1),当x∈[-l,1)时,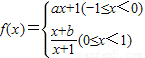 (a,b>0),若
(a,b>0),若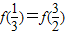 ,则
,则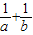 的最小值为( )
的最小值为( )A.1
B.2
C.
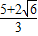
D.
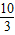
【答案】分析:先利用函数的性质及分段函数的解析式求出2a+3b=3,于是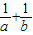 =(
=(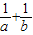 )×
)× (2a+3b),展开利用基本不等式的性质即可.
(2a+3b),展开利用基本不等式的性质即可.
解答:解:由题意得,f( )=f(
)=f( +1)=f(
+1)=f(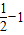 )=f(-
)=f(- )=-
)=- a+1,
a+1,
f( )=
)=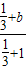 =
=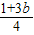 ,
,
由于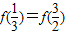 ,
,
∴- a+1=
a+1=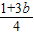 ,即2a+3b=3,
,即2a+3b=3,
则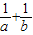 =(
=(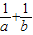 )×
)× (2a+3b)=
(2a+3b)= (5+
(5+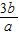 +
+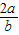 )≥
)≥ (5+2
(5+2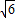 )
)
当且仅当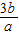 =
=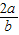 时取等号,
时取等号,
故则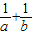 的最小值为
的最小值为 (5+2
(5+2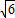 )
)
故选C.
点评:本题主要考查了函数与方程的综合运用,基本不等式等.将原式乘1后再利用基本不等式是解题的关键.
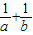 =(
=(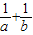 )×
)× (2a+3b),展开利用基本不等式的性质即可.
(2a+3b),展开利用基本不等式的性质即可.解答:解:由题意得,f(
 )=f(
)=f( +1)=f(
+1)=f(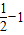 )=f(-
)=f(- )=-
)=- a+1,
a+1,f(
 )=
)=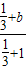 =
=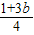 ,
,由于
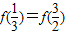 ,
,∴-
 a+1=
a+1=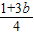 ,即2a+3b=3,
,即2a+3b=3,则
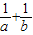 =(
=(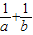 )×
)× (2a+3b)=
(2a+3b)= (5+
(5+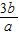 +
+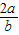 )≥
)≥ (5+2
(5+2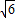 )
)当且仅当
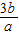 =
=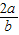 时取等号,
时取等号,故则
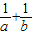 的最小值为
的最小值为 (5+2
(5+2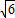 )
)故选C.
点评:本题主要考查了函数与方程的综合运用,基本不等式等.将原式乘1后再利用基本不等式是解题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目