题目内容
在平面直角坐标系xOy中,点P到两点 ,
, 的距离之和等于4,设点P的轨迹为C.
的距离之和等于4,设点P的轨迹为C.
(Ⅰ)写出C的方程;
(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时 ⊥
⊥ ?此时
?此时 的值是多少?.
的值是多少?.
考点: 直线与圆锥曲线的综合问题.
解:
(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以 为焦点,
为焦点,
长半轴为2的椭圆.它的短半轴 ,
,
故曲线C的方程为 .(4分)
.(4分)
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足
消去y并整理得(k2+4)x2+2kx﹣3=0,
故 .(6分)
.(6分)
 ,即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,
,即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,
于是 .
.
所以 时,x1x2+y1y2=0,故
时,x1x2+y1y2=0,故 .(8分)
.(8分)
当 时,
时, ,
, .
. ,
,
而(x2﹣x1)2=(x2+x1)2﹣4x1x2= ,
,
所以 .(12分)
.(12分)

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 到实数集
到实数集 的映射过程:区间
的映射过程:区间 中的实数
中的实数 对应数上的点
对应数上的点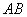 围成一个圆,使两端点
围成一个圆,使两端点 恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 与
与 轴交于点
轴交于点 ,则
,则 ,记作
,记作 .
.
 的解是
的解是
 ; ②
; ② ;
;  是奇函数; ④
是奇函数; ④ 对称.
对称. =
=  +z2在复平面上对应的点位于( )
+z2在复平面上对应的点位于( )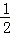 ,求正四棱柱ABCD﹣A1B1C1D1的体积.
,求正四棱柱ABCD﹣A1B1C1D1的体积.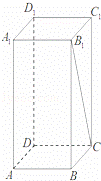
 是
是 成立的_____ _________条件。
成立的_____ _________条件。 对自己的储蓄卡的密码的概率是_____
对自己的储蓄卡的密码的概率是_____ 来估计
来估计 总体的标准差,则总体标准差的估计值是__
总体的标准差,则总体标准差的估计值是__ 的前
的前 项和为
项和为 ,已知
,已知 成等差数列,则等比数
成等差数列,则等比数 列
列