Question

【题目】已知f（x）=ln（x+m）﹣mx．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）设m＞1，x1 ， x2为函数f（x）的两个零点，求证：x1+x2＜0．

Answer 1

【答案】解：（Ⅰ）∵f（x）=ln（x+m）﹣mx，∴ ，
当m≤0时，∴ ，
即f（x）的单调递增区间为（﹣m，+∞），无减区间；
当m＞0时，∴ ，
由f'（x）=0，得 ，
时，f'（x）＞0，
时，f'（x）＜0，
∴m＞0时，易知f（x）的单调递增区间为 ，单调递减区间为 ，
（Ⅱ）由（Ⅰ）知f（x）的单调递增区间为 ，单调递减区间为 ．
不妨设﹣m＜x1＜x2 ， 由条件知 ，即 ，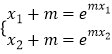
构造函数g（x）=emx﹣x，g（x）=emx﹣x与y=m图象两交点的横坐标为x1 ， x2 ，
由g'（x）=emx﹣1=0可得 ，
而m2＞lnm（m＞1），∴
知g（x）=emx﹣x在区间 上单调递减，在区间 上单调递增．
可知
欲证x1+x2＜0，只需证 ，即证 ，
考虑到g（x）在 上递增，只需证
由g（x2）=g（x1）知，只需证
令 ，
则 ，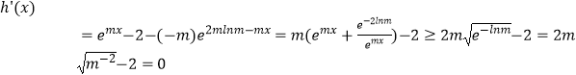
即h（x）单增，又 ，
结合 知h（x1）＜0，即 成立，
即x1+x2＜0成立
【解析】（Ⅰ）求出函数的导数，通过讨论m的范围，求出函数的单调区间即可；（Ⅱ）构造函数g（x）=emx﹣x，g（x）=emx﹣x与y=m图象两交点的横坐标为x1 ， x2 ， 问题转化为证明 令 ，根据函数的单调性证明即可．
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能正确解答此题．