题目内容
【题目】已知函数![]() 是定义在
是定义在![]() 的偶函数,且
的偶函数,且![]() .当
.当![]() 时,
时,![]() ,若方程
,若方程![]() 有300个不同的实数根,则实数m的取值范围为( )
有300个不同的实数根,则实数m的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
首先由已知确定函数![]() 的周期是4,利用导数研究
的周期是4,利用导数研究![]() 在
在![]() 上的性质,单调性、极值,结合偶函数性质作出
上的性质,单调性、极值,结合偶函数性质作出![]() 在
在![]() 上的图象,
上的图象,![]() 的定义域是
的定义域是![]() 含有50个周期,方程
含有50个周期,方程![]() 有300个不同的实数根,那么在
有300个不同的实数根,那么在![]() 的一个周期内有6个根,令
的一个周期内有6个根,令![]() ,可知方程
,可知方程![]() 有两个不等实根
有两个不等实根![]() ,且
,且![]() ,
,![]() ,由二次方程根的分布知识可得解.
,由二次方程根的分布知识可得解.
由![]() 知函数的周期为4,当
知函数的周期为4,当![]() 时,
时,![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递减,当
递减,当![]() 时,
时,![]() ,
,![]() 递增,
递增,![]() ,又
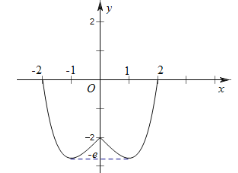
,又![]() 是偶函数,作出
是偶函数,作出![]() 在
在![]() 上的图象,如图.
上的图象,如图.
函数![]() 的周期是4,定义域为
的周期是4,定义域为![]() ,含有50个周期,
,含有50个周期,
方程![]() 有300个不同的实数根,因此在一个周期内有6个根(这里
有300个不同的实数根,因此在一个周期内有6个根(这里![]() ,
,![]() 不是方程的根).
不是方程的根).
令![]() ,方程
,方程![]() 有两个不等实根
有两个不等实根![]() ,且
,且![]() ,
,![]() ,设
,设![]() ,则
,则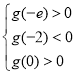 ,解得
,解得![]() .
.
故选:A.

【题目】某校高三年级有500名学生,为了了解数学学科的学习情况,现随机抽出若干名学生在一次测试中的数学成绩(满分150分),制成如下频率分布表:
分组 | 频数 | 频率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 12 | 0.300 |
| 0.275 | |
| 4 | ③ |
| 0.050 | |
合计 | ④ |
(1)①②③④处应分别填什么?
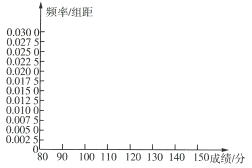
(2)根据频率分布表完成频率分布直方图.
(3)试估计该校高三年级在这次测试中数学成绩的平均分.
【题目】某客户准备在家中安装一套净水系统,该系统为三级过滤,使用寿命为十年.如图所示,两个一级过滤器采用并联安装,二级过滤器与三级过滤器为串联安装。

其中每一级过滤都由核心部件滤芯来实现。在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立),三级滤芯无需更换,若客户在安装净水系统的同时购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.若客户在使用过程中单独购买滤芯,则一级滤芯每个
元.若客户在使用过程中单独购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据
元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据![]() 套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据
套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据![]() 个一级过滤器更换的滤芯个数制成的柱状图,表是根据
个一级过滤器更换的滤芯个数制成的柱状图,表是根据![]() 个二级过滤器更换的滤芯个数制成的频数分布表.
个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表
二级滤芯更换的个数 |
|
|
频数 |
|
|
以![]() 个一级过滤器更换滤芯的频率代替
个一级过滤器更换滤芯的频率代替![]() 个一级过滤器更换滤芯发生的概率,以
个一级过滤器更换滤芯发生的概率,以![]() 个二级过滤器更换滤芯的频率代替
个二级过滤器更换滤芯的频率代替![]() 个二级过滤器更换滤芯发生的概率.
个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为![]() 的概率;
的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() ,
,![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() ,
,![]() 的值.
的值.
