题目内容
已知点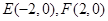 ,曲线
,曲线 上的动点
上的动点 满足
满足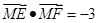 ,定点
,定点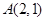 ,由曲线
,由曲线 外一点
外一点 向曲线
向曲线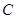 引切线
引切线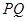 ,切点为
,切点为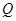 ,且满足
,且满足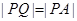 .
.

(1)求线段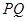 长的最小值;
长的最小值;
(2)若以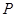 为圆心所作的圆
为圆心所作的圆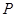 与曲线
与曲线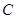 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆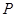 的标准方程.
的标准方程.
【答案】
(1)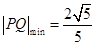 ;(2)
;(2)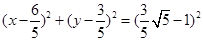 .
.
【解析】
试题分析:本题主要考查圆的标准方程和几何性质、直线的方程、向量的点乘、平面内两点间距离公式等基础知识.考查数形结合的数学思想.考查运算求解能力、综合分析和解决问题的能力.第一问,利用向量的点乘求出点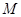 的轨迹方程,数形结合找出
的轨迹方程,数形结合找出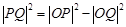 ,所以
,所以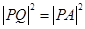 ,然后配方法求最值;第二问,利用两圆的位置关系列出不等式,用配方法求最值,得到圆心和半径,写出圆的标准方程.
,然后配方法求最值;第二问,利用两圆的位置关系列出不等式,用配方法求最值,得到圆心和半径,写出圆的标准方程.
试题解析:(Ⅰ)设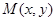 ,则
,则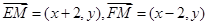 ,
,
∴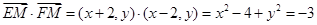 ,
,
即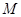 点轨迹(曲线
点轨迹(曲线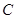 )方程为
)方程为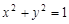 ,即曲线
,即曲线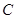 是
是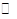
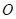 . 2分
. 2分
连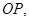 ∵
∵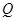 为切点,
为切点,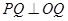 ,由勾股定理有:
,由勾股定理有: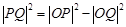 .
.
又由已知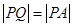 ,故
,故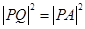 .
.
即: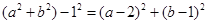 ,
,
化简得实数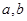 间满足的等量关系为:
间满足的等量关系为: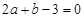 ,即
,即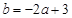 .(4分)
.(4分)
∴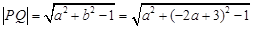
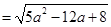 =
=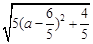 ,
,
故当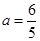 时,
时,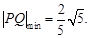 即线段
即线段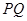 长的最小值为
长的最小值为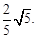 7分
7分
(另法)由点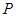 在直线
在直线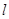 :
: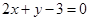 上.
上.
∴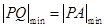 ,即求点
,即求点 到直线
到直线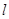 的距离.
的距离.
∴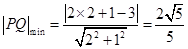 (7分)
(7分)
(Ⅱ)设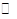
 的半径为
的半径为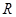 ,∵
,∵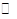
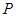 与
与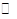
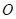 有公共点,
有公共点,
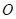 的半径为1,
的半径为1,
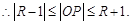 即
即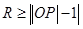 且
且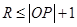 . 8分
. 8分
而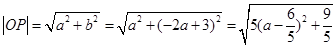 , 9分
, 9分
故当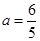 时,
时,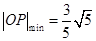 . 10分
. 10分
此时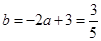 ,
,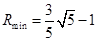 . 11分
. 11分
得半径取最小值时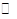
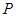 的标准方程为
的标准方程为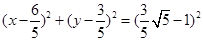 . 13分
. 13分
(另法)
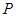 与
与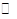
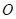 有公共点,
有公共点,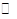
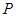 半径最小时为与
半径最小时为与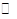
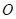 外切(取小者)的情形,而这些半径的最小值为圆心
外切(取小者)的情形,而这些半径的最小值为圆心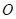 到直线
到直线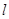 的距离减去1,圆心
的距离减去1,圆心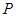 为过原点与
为过原点与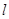 垂直的直线
垂直的直线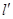 与
与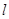 的交点
的交点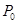 .
.
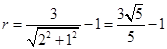 .
.
又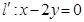 ,(10分)
,(10分)
解方程组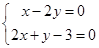 ,得
,得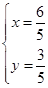 .即
.即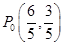 ,
,
∴所求
 标准方程为
标准方程为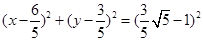 .(13分)
.(13分)
考点:1.向量的点乘;2.圆的标准方程;3.勾股定理;4.配方法求最值.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
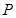 为圆
为圆 上的动点,且
上的动点,且 轴上,
轴上,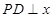 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线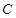 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 、
、 两点。
两点。 ,使得
,使得 总能被
总能被 为圆
为圆 上的动点,且
上的动点,且 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 、
、 两点。
两点。 ,使得
,使得 总能被
总能被 为曲线
为曲线 在圆
在圆 上,
上, ,曲线
,曲线
 ,直线
,直线 , ………………3分
, ………………3分  ,可得
,可得 
 ,∴
,∴
 ,
,  ,则
,则 ,
,  得到。
得到。 ,
, ,
, , ………………10分
, ………………10分 ,
, ,
,  ,即只要
,即只要 ………………12分
………………12分  时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 ,使得
,使得 总能被
总能被 轴平分
轴平分 为圆
为圆 上的动点,且
上的动点,且 轴上,
轴上,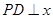 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 、
、 两点。
两点。 ,使得
,使得 总能被
总能被