题目内容
考察正方体6个面的中心，甲从这6个点中任意选两个点连成直线，乙也从这6个点中任意选两个点连成直线，则所得的两条直线相互平行但不重合的概率等于( )
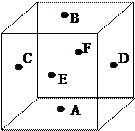
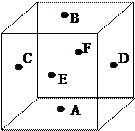
A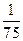． | B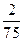． | C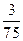． | D． |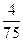
D
甲从这6个点中任意选两个点连成直线，乙也从这6个点中任意选两个点连成直线，共有
种不同取法，其中所得的两条直线相互平行但不重合有
共12对，所以所求概率为
，选D.
种不同取法，其中所得的两条直线相互平行但不重合有共12对，所以所求概率为，选D.
练习册系列答案
相关题目
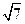
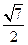
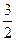
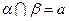，α⊥γ，β⊥γ，b∥α，b∥β．
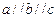，则直线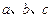
至多可以确定平面的个数为 （ ）
