题目内容
在一个塔底的水平面上某点测得该塔顶的仰角为θ,由此点向塔底沿直线行走了30 m,测得塔顶的仰角为2θ,再向塔底前进10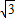 m,又测得塔顶的仰角为4θ,则塔的高度为 .
m,又测得塔顶的仰角为4θ,则塔的高度为 .
【答案】分析:先根据题意确定PA、PB、PC和BC的值,在△BPC中应用余弦定理可求得cos2θ的值,进而可确定2θ的值,然后在△PCD中可求得PD的长度,从而确定答案.
解答: 解:如图,依题意有PB=BA=30,PC=BC=
解:如图,依题意有PB=BA=30,PC=BC= .在△BPC中,由余弦定理可得
.在△BPC中,由余弦定理可得
cos2θ= =
= ,
,
所以2θ=30°,4θ=60°,
在△PCD中,
可得PD=PC•sin4θ=10 •
• =15(m).
=15(m).
故答案为:15m
点评:本题主要考查余弦定理的应用.考查应用余弦定理解决实际问题的能力.
解答:
 解:如图,依题意有PB=BA=30,PC=BC=
解:如图,依题意有PB=BA=30,PC=BC= .在△BPC中,由余弦定理可得
.在△BPC中,由余弦定理可得cos2θ=
 =
= ,
,所以2θ=30°,4θ=60°,
在△PCD中,
可得PD=PC•sin4θ=10
 •
• =15(m).
=15(m).故答案为:15m
点评:本题主要考查余弦定理的应用.考查应用余弦定理解决实际问题的能力.

练习册系列答案
相关题目
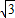 m,又测得塔顶的仰角为4θ,则塔的高度为 .
m,又测得塔顶的仰角为4θ,则塔的高度为 .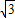 m,又测得塔顶的仰角为4θ,则塔的高度为 .
m,又测得塔顶的仰角为4θ,则塔的高度为 .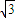 m,又测得塔顶的仰角为4θ,则塔的高度为 .
m,又测得塔顶的仰角为4θ,则塔的高度为 .