题目内容
(本小题14分)
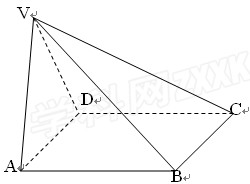
如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,
平面VAD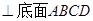
(1)证明:AB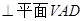 ;
;
(2)求面VAD与面VDB所成的二面角的余弦值。
【答案】
方法一:(用传统方法)(1)证明:平面VAD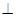 平面ABCD,AB
平面ABCD,AB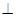 AD,AB
AD,AB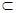 平面ABCD,
平面ABCD,
面VAD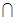 ABCD=AD,
ABCD=AD,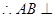 面VAD
面VAD
(2) 取VD中点E,连接AE,BE,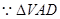 是正三角形,
是正三角形,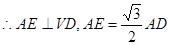
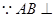 面VAD, AE,
面VAD, AE,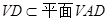
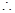 AB
AB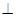 VD,AB
VD,AB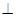 AE
AE
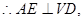 AB
AB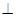 VD, AB
VD, AB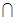 AE=A,且AB,AE
AE=A,且AB,AE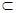 平面ABE,
平面ABE, 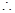 VD
VD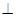 平面ABE,
平面ABE,
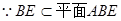 ,
,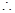 BE
BE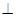 VD,
VD,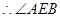 是所求的二面角的平面角。
是所求的二面角的平面角。
在RT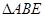 中,
中,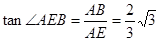 ,
,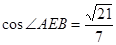
方法二:(空间向量法)以D为坐标原点,建立空间直角坐标系如图。
(1)证明:不妨设A(1,0,0),
B(1,1,0), 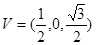 ,
,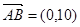 ,
,
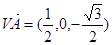 ,
,
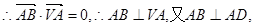 因此AB与平面VAD内两条相交直线VA,AD都垂直,
因此AB与平面VAD内两条相交直线VA,AD都垂直,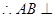 面VAD
面VAD
(2)取VD的中点E,则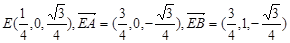 ,
,
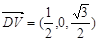 ,由
,由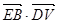 =0,得
=0,得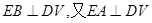 ,因此
,因此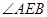 是所求二面角的平面角。
是所求二面角的平面角。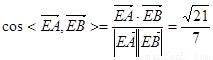
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
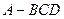 中,
中,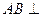 平面
平面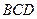 ,
,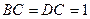 ,
,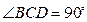 ,
,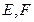 分别是
分别是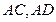 上
上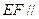 平面
平面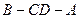 为
为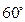 .
.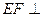 平面
平面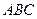 ;
;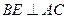 ,求直线
,求直线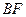 与平面
与平面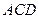 所成角的余弦值.
所成角的余弦值.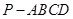 中,底面
中,底面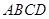 为矩形,侧棱
为矩形,侧棱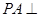 底面
底面 为
为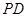 的中点.
的中点.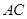 与
与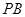 所成角的余弦值;
所成角的余弦值;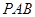 内找一点
内找一点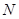 ,使
,使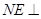 平面
平面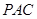 ,并分别求出点
,并分别求出点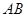 和
和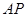 的距离.
的距离.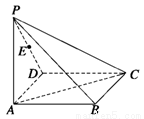
 中,
中, ,点
,点 在边
在边 上,
上, 。
。 平面
平面 ;
; 是
是 的中点,求证:
的中点,求证: 平面
平面 .
.