题目内容
20．医院打算从5名外科医生，4名内科医生，3名脑科医生中，选出2名不同科的医生到山区进行义诊，问有多少种不同的选派方式？分析 由题意分三类，第一类，1名外科医生，1名内科医生，第二类，1名外科医生，1名脑科医生，第三类，1名内科医生，1名脑科医生，根据分类计数原理可得．
解答 解：第一类，1名外科医生，1名内科医生，共有5×4=20种，
第二类，1名外科医生，1名脑科医生，共有4×3=12种，
第三类，1名内科医生，1名脑科医生，共有5×3=15种，
根据分类计数原理，共有20+12+15=47种，
故选出2名不同科的医生到山区进行义诊，有47种不同的选派方式．
点评 本题主要考查了分类分步计数原理，如何分类是关键，属于基础题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
10．设A，B，C，D是平面上互异的四个点，若（$\overrightarrow{DB}$+$\overrightarrow{DC}$-2$\overrightarrow{DA}$）•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）=0，则△ABC的形状是（ ）
| A． | 直角三角形 | B． | 等腰三角形 | C． | 锐角三角形 | D． | 钝角三角形 |
11．2015年12月27日全国人大常委会表决通过了人口与计划生育法修正案全面二孩定于20I6年1月1日起正式实施，为了解适龄民众对放开生育二胎政策的态度，某机构从某市选取70后和80后作为调查对象．随机调查了100位，得到数据如下表：
（1）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若以该市70后公民中随机抽取3位，记其中生二孩的人数为X，求随机变量X的分布列和数学期望．
（2）根据调查数据，是否在犯错误的概率不超过0.1的前提下（有90%以上自把握）认为“生二孩与年龄有关”？并说明理由．
| 生二孩 | 不生二孩 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
（2）根据调查数据，是否在犯错误的概率不超过0.1的前提下（有90%以上自把握）认为“生二孩与年龄有关”？并说明理由．
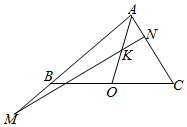如图所示，在△ABC中，AO是BC边上的中线，K为AO上一点，且$\overrightarrow{AO}$=2$\overrightarrow{AK}$，过点K的直线分别交直线AB、AC于不同的两点M，N，若$\overrightarrow{AB}$=m$\overrightarrow{AM}$，$\overrightarrow{AC}$=n$\overrightarrow{AN}$，则m+n=4．
10．（2003年）已知sinα•cosα=-$\frac{1}{5}$，则cos4α的值为（ ）
| A． | $\frac{1}{25}$ | B． | $\frac{8}{25}$ | C． | $\frac{17}{25}$ | D． | $\frac{24}{25}$ |