题目内容

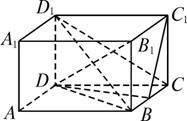
如图ABCD—A1B1C1D1是正四棱柱，侧棱长为1，底面边长为2，E是棱BC的中点.

(1)求三棱锥D1—DBC的体积；

(2)证明BD1∥平面C1DE；

(3)求面C1DE与面CDE所成二面角的正切值.

(1). (2)  同解析     

(3)面C1DE与面CDE所成二面角的正切值为.


解析:

(1)解析：.

(2)证明：记D1C与DC1的交点为O，连结OE.

∵O是CD1的中点，E是BC的中点，∴EO∥BD1.

∵BD1平面C1DE，EO平面C1DE，∴BD1∥平面C1DE.

(3)解析：如图2，过C作CH⊥DE于H，连结C1H.在正四棱柱ABCD-A1B1C1D1中，C1C⊥平面ABCD，∴C1H⊥DE，∠C1HC是面C1DE与面CDE所成二面角的平面角.

∵DC=2，CC1=1，CE=1，

∴

∴tan C1HC=，

即面C1DE与面CDE所成二面角的正切值为.

练习册系列答案
相关题目
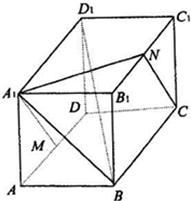
精英家教网如图，长方体ABCD-A1B1C1D1中，AB=A1A=a，BC=
2
a，M是AD中点，N是B1C1中点．
（1）求证：A1、M、C、N四点共面；
（2）求证：BD1⊥MCNA1；
（3）求证：平面A1MNC⊥平面A1BD1；
（4）求A1B与平面A1MCN所成的角．
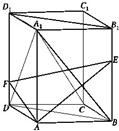精英家教网如图，在长方体ABCD-A1B1C1D1中，点E、F分别BB1、DD1上，且AE⊥A1B，AF⊥A1D．
（1）求证：A1C⊥平面AEF；
（2）若规定两个平面所成的角是这两个平面所组成的二面角中的锐角（或直角），则在空间中有定理：若两条直线分别垂直于两个平面，则这两条直线所成的角与这两个平面所成的角相等．
试根据上述定理，在AB=4，AD=3，AA1=5时，求平面AEF与平面D1B1BD所成的角的大小．（用反三角函数值表示）
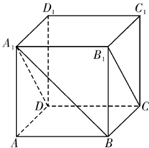精英家教网如图，在正方体ABCD-A1B1C1D1中，棱长为a，M、N分别为A1B和AC上的点，A1M=AN=
2
a
3
，则MN与平面BB1C1C的位置关系是（　　）
A、相交B、平行
C、垂直D、不能确定
精英家教网如图，在正方体ABCD-A1B1C1D1中，直线A1B与平面A1B1CD所成的角的大小等于
 
．
（2007•无锡二模）如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形，AB∥CD，AB⊥AD，AB=AD=A1B=2CD，侧面A1ADD1为正方形．
（1）求直线A1A与底面ABCD所成角的大小；
（2）求二面角C-A1B-A正切值的大小；
（3）在棱C1C上是否存在一点P，使得 D1P∥平面A1BC，若存在，试说明点P的位置；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网