题目内容
求证:-1≤
证法一:要证-1≤![]() <1,只需证-a2-1≤a2-1<a2+1,
<1,只需证-a2-1≤a2-1<a2+1,
也就是证2a2≥0且-1<1.
由于2a2≥0,且-1<1成立,故-1≤![]() <1成立.
<1成立.
证法二:要证-1≤![]() <1,只需证
<1,只需证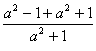 ≥0,即
≥0,即![]() ≥0.
≥0.
上式显然成立,所以![]() ≥-1.类似地,可以证明
≥-1.类似地,可以证明![]() <1,故-1≤
<1,故-1≤![]() <1成立.
<1成立.

练习册系列答案
相关题目
题目内容
求证:-1≤
证法一:要证-1≤![]() <1,只需证-a2-1≤a2-1<a2+1,
<1,只需证-a2-1≤a2-1<a2+1,
也就是证2a2≥0且-1<1.
由于2a2≥0,且-1<1成立,故-1≤![]() <1成立.
<1成立.
证法二:要证-1≤![]() <1,只需证
<1,只需证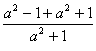 ≥0,即
≥0,即![]() ≥0.
≥0.
上式显然成立,所以![]() ≥-1.类似地,可以证明
≥-1.类似地,可以证明![]() <1,故-1≤
<1,故-1≤![]() <1成立.
<1成立.
