题目内容
已知双曲线的方程为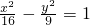 ,则双曲线的离心率是________.
,则双曲线的离心率是________.

分析:由题意可得ab的值,进而可得c的值,由离心率的定义可得答案.
解答:由题意可得a=4,b=3,c=
 =5,
=5,故其离心率为e=
 =
= ,
,故答案为:

点评:本题考查双曲线的离心率,属基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
题目内容
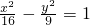 ,则双曲线的离心率是________.
,则双曲线的离心率是________.
 =5,
=5, =
= ,
,

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案