题目内容
20.函数f(x)=|x|+$\frac{a}{x^2}$(其中a∈R)的图象不可能是( )| A. |  | B. |  | ||
| C. | 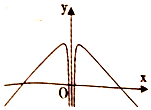 | D. |  |
分析 通过a的取值,判断对应的函数的图象,即可推出结果.
解答 解:当a=0时,函数f(x)=|x|+$\frac{a}{x^2}$=|x|,函数的图象可以是B.
当a=1时,函数f(x)=|x|+$\frac{a}{x^2}$=|x|+$\frac{1}{{x}^{2}}$,函数的图象可以类似A;
当a=-1时,函数f(x)=|x|+$\frac{a}{x^2}$=|x|-$\frac{1}{{x}^{2}}$,x>0时,|x|-$\frac{1}{{x}^{2}}$=0只有一个实数根x=1,函数的图象可以是D;
所以函数的图象不可能是C.
故选:C.
点评 本题考查函数的图象的判断,特殊值法是解答本题简单方法之一,是中档题.

练习册系列答案
相关题目
15.若$sin({x+\frac{π}{6}})=\frac{1}{3}$,则$tan({2x+\frac{π}{3}})$等于( )
| A. | $\frac{7}{9}$ | B. | $±\frac{7}{9}$ | C. | $\frac{{4\sqrt{2}}}{7}$ | D. | $±\frac{{4\sqrt{2}}}{7}$ |
10.直线kx-y+1=3k中,无论k如何变动,直线都恒过定点( )
| A. | (0,0) | B. | (0,1) | C. | (3,1) | D. | (2,1) |
 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.