题目内容
已知向量a=(1,1,-2),b= ,若a•b≥0,则实数x的取值范围为
,若a•b≥0,则实数x的取值范围为
- A.

- B.
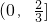
- C.(-∞,0)∪
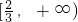
- D.(-∞,0]∪
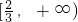
C
分析:先利用向量数量积的坐标运算得出 ,再解关于x 的不等式即可.
,再解关于x 的不等式即可.
解答:由 =(1,1,-2),
=(1,1,-2), =
= ,
,
 =3-
=3-
根据 ≥0,得出3-
≥0,得出3- ≥0
≥0
即 ≥0
≥0
化为x(3x-2)≥0且x≠0
解得x∈(-∞,0)∪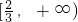
故选C
点评:本题考查向量数量积的坐标运算,不等式的解法.本题中涉及到分式不等式求解,一般化为整式不等式求解.
分析:先利用向量数量积的坐标运算得出
 ,再解关于x 的不等式即可.
,再解关于x 的不等式即可.解答:由
 =(1,1,-2),
=(1,1,-2), =
= ,
, =3-
=3-
根据
 ≥0,得出3-
≥0,得出3- ≥0
≥0即
 ≥0
≥0化为x(3x-2)≥0且x≠0
解得x∈(-∞,0)∪
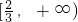
故选C
点评:本题考查向量数量积的坐标运算,不等式的解法.本题中涉及到分式不等式求解,一般化为整式不等式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(1,1),
=(2,n),若
⊥
,则n等于( )
| a |
| b |
| a |
| b |
| A、-3 | B、-2 | C、1 | D、2 |