题目内容
 如图所示,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=105°,∠CBA=45°,且AB=100m.
如图所示,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=105°,∠CBA=45°,且AB=100m.(1)求sin∠CAB的值;
(2)求该河段的宽度.
分析:(1)由题意,利用两角和的正弦公式,结合特殊角的三角函数值加以计算即可得sin∠CAB的值;
(2)由题意画出简图,在三角形中利用正弦定理先求出BC的长度,然后过点C作CD垂直于对岸,垂足为D,由题意可得CD的长就是该河段的宽度,解出△ACB的BC长后再在△BDC中即可解出BD长,可得该河段的宽度..
(2)由题意画出简图,在三角形中利用正弦定理先求出BC的长度,然后过点C作CD垂直于对岸,垂足为D,由题意可得CD的长就是该河段的宽度,解出△ACB的BC长后再在△BDC中即可解出BD长,可得该河段的宽度..
解答:解:(1)sin∠CAB=sin(60°+45°)=sin60°cos45°+cos60°sin45°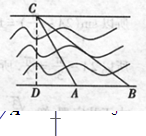
=
×
+
×
=
;
(2)∵∠CAB=105°,∠CBA=45°
∴∠ACB=180°-∠CAB-∠CBA=30°,
由正弦定理得
=
,
得BC=
=50(
+
)(m),
如图过点C作CD垂直于对岸,垂足为D,则CD的长就是该河段的宽度.
∵在Rt△BDC中,∠BCD=∠CBA=45°,
∴BD=BCsin45°=50(
+
)•
=50(
+1)(m).
答:(1)求sin∠CAB的值为
;(2)该河段的宽度为50(
+1)(m).

=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
(2)∵∠CAB=105°,∠CBA=45°
∴∠ACB=180°-∠CAB-∠CBA=30°,
由正弦定理得
| AB |
| sin∠ACB |
| BC |
| sin∠CAB |
得BC=
| ABsin105° |
| sin30° |
| 6 |
| 2 |
如图过点C作CD垂直于对岸,垂足为D,则CD的长就是该河段的宽度.
∵在Rt△BDC中,∠BCD=∠CBA=45°,
∴BD=BCsin45°=50(
| 6 |
| 2 |
| ||
| 2 |
| 3 |
答:(1)求sin∠CAB的值为
| ||||
| 4 |
| 3 |
点评:本题给出实际问题,求河岸的宽度,着重考查了学生对题意的理解,还考查了正弦定理解三角形,两角和的正弦公式,查了学生的计算能力,属于基础题.

练习册系列答案
相关题目
 如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米均不小于2米,且要求“转角处(图中矩形AEFG)”的面积为8平方米
如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米均不小于2米,且要求“转角处(图中矩形AEFG)”的面积为8平方米 (2013•枣庄二模)如图所示是某算法的程序框图,则程序运行后输出的结果是( )
(2013•枣庄二模)如图所示是某算法的程序框图,则程序运行后输出的结果是( )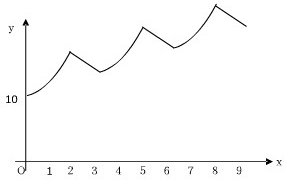 (2008•徐汇区二模)随着国民经济的日益发展和居民财富的不断积累,理财观念日益深入人心.投资股市正成为一种时尚,如图所示是某股票的K线图(即股票价格的走势图),其起始价格为每股10元.假设其运行规律为两个月上涨,接下来一个月下跌,上行线是以每月10%递增的指数型曲线段,下行线是以-1为斜率的直线型线段;设第n月末的股票价格为f(n).
(2008•徐汇区二模)随着国民经济的日益发展和居民财富的不断积累,理财观念日益深入人心.投资股市正成为一种时尚,如图所示是某股票的K线图(即股票价格的走势图),其起始价格为每股10元.假设其运行规律为两个月上涨,接下来一个月下跌,上行线是以每月10%递增的指数型曲线段,下行线是以-1为斜率的直线型线段;设第n月末的股票价格为f(n).