题目内容
已知函数
(1)当
(2)当 时,讨论
时,讨论 的单调性.
的单调性.
解:(1) 当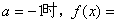
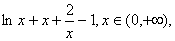
所以 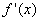
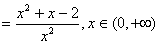
因此,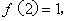
即 曲线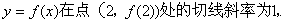
又 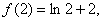
所以曲线

(2)因为 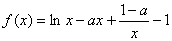 ,
,
所以 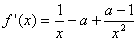
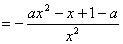
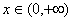 ,
,
令 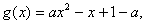
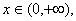
(1)当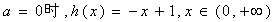
所以,当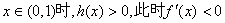 ,函数
,函数 单调递减;
单调递减;
当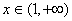 时,
时,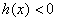 ,此时
,此时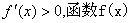 单调递
单调递
(2)当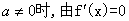
即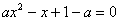 ,解得
,解得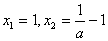
①当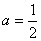 时,
时,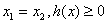 恒成立,
恒成立,
此时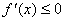 ,函数
,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;
②当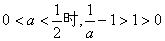
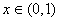 时,
时,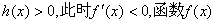 单调递减;
单调递减;
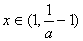 时,
时,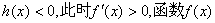 单调递增;
单调递增;
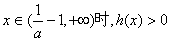 ,此时
,此时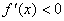 ,函数
,函数 单调递减;
单调递减;
③当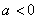 时,由于
时,由于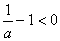
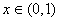 时,
时,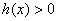 ,此时
,此时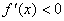 ,函数
,函数 单调递减;
单调递减;
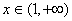 时,
时,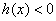 ,此时
,此时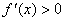 ,函数
,函数 单调递增。
单调递增。
综上所述:
当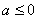 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在(1,+∞)上单调递增;
在(1,+∞)上单调递增;
当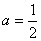 时,函数
时,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;
当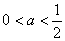 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在
在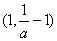 上单调递增;
上单调递增;
函数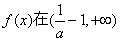 上单调递减,
上单调递减,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在R上定义运算 若对任意
若对任意 ,不等式
,不等式 都成立,则实数
都成立,则实数 的取值范围是( )
的取值范围是( )
| A. | B. | |||
| C. | D. |
 在
在 方向上的投影为( )
方向上的投影为( ) (B)
(B) (C)-
(C)-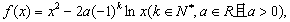
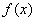 的单调性;
的单调性;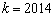 时,关于
时,关于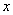 的方程
的方程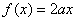 有唯一解,求
有唯一解,求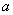 的值;
的值;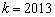 时,证明: 对一切
时,证明: 对一切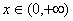 ,都有
,都有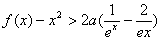 成立.
成立.



 中,
中, ,
, ,
, ,
,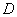 是边
是边 上一点,
上一点, ,则
,则
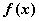 的导函数为
的导函数为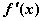 ,函数
,函数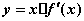 的图象的一部分如图所示,则
的图象的一部分如图所示,则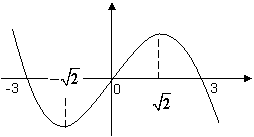

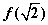 ,极小值为
,极小值为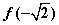
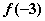 ,极小值为
,极小值为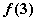
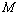 由满足:对任意
由满足:对任意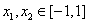 时,都有
时,都有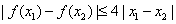 的函数
的函数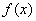 组成.对于两个函数
组成.对于两个函数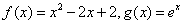 ,以下关系成立的是
,以下关系成立的是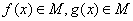 B.
B.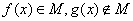
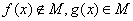 D.
D.