题目内容
设函数 .
.
(1)当a=0时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)若函数f(x)在区间[2,3]上单调递减,求a的取值范围.
解:(1)a=0时, ,∴f′(1)=1
,∴f′(1)=1
∴f(1)= ,∴曲线y=f(x)在点A(1,f(1))处的切线方程为y-
,∴曲线y=f(x)在点A(1,f(1))处的切线方程为y- =x-1,即
=x-1,即
(2) ,记g(x)=x2+(1-a)x+a-1
,记g(x)=x2+(1-a)x+a-1
∵函数f(x)在区间[2,3]上单调递减
∴x2+(1-a)x+a-1≤0在区间[2,3]上恒成立
∴ ,∴
,∴
∴a≥ .
.
分析:(1)求导函数,确定确定坐标,与切线的斜率,即可求得切线方程;
(2)求导数 ,记g(x)=x2+(1-a)x+a-1,利用函数f(x)在区间[2,3]上单调递减,可得x2+(1-a)x+a-1≤0在区间[2,3]上恒成立,从而可建立不等式组,即可求a的取值范围.
,记g(x)=x2+(1-a)x+a-1,利用函数f(x)在区间[2,3]上单调递减,可得x2+(1-a)x+a-1≤0在区间[2,3]上恒成立,从而可建立不等式组,即可求a的取值范围.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,正确求导是关键.
 ,∴f′(1)=1
,∴f′(1)=1∴f(1)=
 ,∴曲线y=f(x)在点A(1,f(1))处的切线方程为y-
,∴曲线y=f(x)在点A(1,f(1))处的切线方程为y- =x-1,即
=x-1,即
(2)
 ,记g(x)=x2+(1-a)x+a-1
,记g(x)=x2+(1-a)x+a-1∵函数f(x)在区间[2,3]上单调递减
∴x2+(1-a)x+a-1≤0在区间[2,3]上恒成立
∴
 ,∴
,∴
∴a≥
 .
.分析:(1)求导函数,确定确定坐标,与切线的斜率,即可求得切线方程;
(2)求导数
 ,记g(x)=x2+(1-a)x+a-1,利用函数f(x)在区间[2,3]上单调递减,可得x2+(1-a)x+a-1≤0在区间[2,3]上恒成立,从而可建立不等式组,即可求a的取值范围.
,记g(x)=x2+(1-a)x+a-1,利用函数f(x)在区间[2,3]上单调递减,可得x2+(1-a)x+a-1≤0在区间[2,3]上恒成立,从而可建立不等式组,即可求a的取值范围.点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,正确求导是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求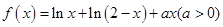 。
。 的单调区间。
的单调区间。 上的最大值为
上的最大值为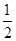 ,求a的值。
,求a的值。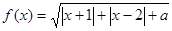 。
。 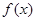 的定义域。
的定义域。 。
。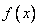 的单调区间。
的单调区间。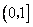 上的最大值为
上的最大值为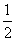 ,求a的值。
,求a的值。