题目内容
位于北纬x度的A、B两地经度相差90°，且A、B两地间的球面距离为
R（R为地球半径），那么x等于（ ）
| π |
| 3 |
| A、30 | B、45 | C、60 | D、75 |
分析：先根据题意画出示意图，欲求x，即求A、B两地位于北纬多少度，即图中∠OAQ的大小，根据球面距离计算出∠AOB，再结合直角三角形中的边角关系即可求得x．
解答：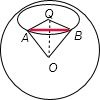
解：根据题意画出示意图，如图．
∵A、B两地间的球面距离为
R（R为地球半径），
∴∠AOB=
=
=
，
∴在三角形AOB中，AO=AB，
∵A、B两地经度相差90°，
∴∠AQB=90°，在直角三角形AQB中，AB=
AQ，
∴在直角三角形AOQ中，AO=
AQ，
∴∠OAQ=45°，
即A、B两地位于北纬45°度，x=45°．
故选B．
解：根据题意画出示意图，如图．∵A、B两地间的球面距离为
| π |
| 3 |
∴∠AOB=
| 球面距离 |
| 球半径 |
| ||
| R |
| π |
| 3 |
∴在三角形AOB中，AO=AB，
∵A、B两地经度相差90°，
∴∠AQB=90°，在直角三角形AQB中，AB=
| 2 |
∴在直角三角形AOQ中，AO=
| 2 |
∴∠OAQ=45°，
即A、B两地位于北纬45°度，x=45°．
故选B．
点评：球面上两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧的长度．（大圆就是经过球心的平面截球面所得的圆）我们把这个弧长叫做两点的球面距离．
练习册系列答案
相关题目
