题目内容
已知P(x,y)为函数y=xsinx+cosx上的任意一点,f(x)为该函数在点P处切线的斜率,则f(x)的部分图象是( )
分析:f(x)为该函数在点P处切线的斜率,结合导数的几何意义,得到f(x)=(xsinx+cosx)′=xcosx.再讨论函数
f(x)的奇偶性,得到函数为奇函数,图象关于原点对称,最后通过验证当0<x<
时,f(x)的符号,可得正
确选项.
f(x)的奇偶性,得到函数为奇函数,图象关于原点对称,最后通过验证当0<x<
| π |
| 2 |
确选项.
解答:解:∵y=xsinx+cosx
∴y′=(xsinx)′+(cosx)′=sinx+xcosx-sinx=xcosx
∵f(x)为该函数在点P处切线的斜率
∴f(x)=xcosx
∵f(-x)=-xcos(-x)=-xcosx=-f(x)
∴函数y=f(x)是奇函数,图象关于原点对称
再根据当0<x<
时,x与cosx均为正值
可得:0<x<
时,f(x)>0,
因此符合题意的图象只有B
故选B
∴y′=(xsinx)′+(cosx)′=sinx+xcosx-sinx=xcosx
∵f(x)为该函数在点P处切线的斜率
∴f(x)=xcosx
∵f(-x)=-xcos(-x)=-xcosx=-f(x)
∴函数y=f(x)是奇函数,图象关于原点对称
再根据当0<x<
| π |
| 2 |
可得:0<x<
| π |
| 2 |
因此符合题意的图象只有B
故选B
点评:本题以含有三角函数表达式的函数为载体,考查了导数的几何意义、函数奇偶性与图象间的联系等知识点,属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |
 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )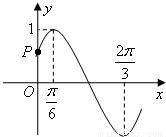



 -2lnx、
-2lnx、