题目内容
【题目】已知椭圆![]() 的中心和抛物线
的中心和抛物线![]() 的顶点都在坐标原点
的顶点都在坐标原点![]() ,
, ![]() 和
和![]() 有公共焦点
有公共焦点![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 的长轴长、短轴长及点
的长轴长、短轴长及点![]() 到直线
到直线![]() 的距离成等比数列。
的距离成等比数列。
(Ⅰ)当![]() 的准线与直线
的准线与直线![]() 的距离为
的距离为![]() 时,求
时,求![]() 及
及![]() 的方程;
的方程;
(Ⅱ)设过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,交
两点,交![]() 于
于![]() ,
, ![]() 两点。当
两点。当![]() 时,求
时,求![]() 的值。
的值。
【答案】(Ⅰ)![]() :
: ![]() ,
, ![]() :
: ![]() (Ⅱ)
(Ⅱ)![]()
【解析】【试题分析】(1)依据题设条件“![]() 的长轴长、短轴长及点
的长轴长、短轴长及点![]() 到直线
到直线![]() 的距离成等比数列”建立方程
的距离成等比数列”建立方程 求得
求得![]() ,从而求出
,从而求出![]() 的右准线方程为
的右准线方程为![]() ,然后借助题设“
,然后借助题设“![]() 的准线与直线
的准线与直线![]() 的距离为
的距离为![]() ”建立方程求出
”建立方程求出![]() ,求出
,求出![]() 及
及![]() 的方程;(2)先建立直线
的方程;(2)先建立直线![]() 的方程
的方程![]() :
: ![]() ,后与椭圆方程联立,借助已知
,后与椭圆方程联立,借助已知![]() 求出
求出![]() 的值,再与曲线
的值,再与曲线![]() 的方程联立求出
的方程联立求出![]() 的值:
的值:
解:(Ⅰ)设![]() :
: ![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
: ![]() .
.
由条件知 ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
, ![]() .
.
从而![]() :
: ![]() ,
, ![]() :
: ![]() .
.
(Ⅱ)由题设知![]() :
: ![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,即
,即![]()
由![]() , 知
, 知![]() 满足
满足 ![]() ,
,
从而![]()
由条件![]() ,得
,得![]() , 故
, 故![]() :
: ![]() .
.
由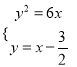 得
得![]() ,所以
,所以![]()
于是![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目