题目内容
【题目】已知球内接正四棱锥![]() 的高为
的高为![]() 相交于
相交于![]() ,球的表面积为
,球的表面积为![]() ,若
,若![]() 为
为![]() 中点.
中点.
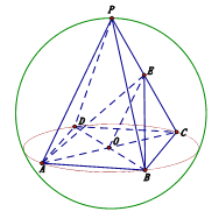
(1)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1) 由球的表面积求出球的半径R,设球心为![]() ,则
,则![]() 必在
必在![]() 上,连
上,连![]() ,根据球的性质有
,根据球的性质有![]() ,求解易得底面边长以及侧棱长,则结论易得;(2)证明
,求解易得底面边长以及侧棱长,则结论易得;(2)证明![]() 平面
平面![]() ,则
,则![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,由
的距离,由![]() ,则结论易得.
,则结论易得.
试题解析:由球的表面积公式![]() ,得球的半径
,得球的半径![]() ,
,
设球心为![]() ,在正四棱锥
,在正四棱锥![]() 中,高为
中,高为![]() ,则
,则![]() 必在
必在![]() 上,
上,
连![]() ,则
,则![]() ,
,
则在![]() ,有
,有![]() ,即
,即![]() ,可得正方形
,可得正方形![]() 的边长为
的边长为![]() ,
,
侧棱![]() .
.
(1)在正方形![]() 中,
中, ![]() ,所
,所![]() 以是异面直线
以是异面直线![]() 和
和![]() 所成的角或其补角,
所成的角或其补角,
取![]() 中点
中点![]() ,在等腰
,在等腰![]() 中,可得
中,可得![]() ,斜高
,斜高![]() ,
,
则在![]() 中,
中, ![]() ,
,
所以异面直线![]() 和
和![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;
;
(2)由![]() 为
为![]() 中点,得
中点,得![]() ,
,
且满足![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,
的距离,
又因为![]() ,
,
再设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则由
,则由![]() ,
,
可得![]() ,则
,则![]() ,
,
所以点![]() 到平面
到平面![]() 的距离
的距离![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目