题目内容
如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
,VC=1,画出(要写出作图过程)二面角V-AB-C的平面角,并求出它的度数.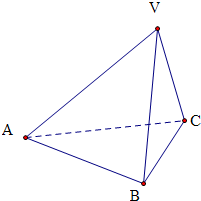
| 3 |

分析:取AB的中点D,连结CD、VD,根据△ABV与△ABC是有公共底边AB的等腰三角形,得到VD⊥AB且CD⊥AB,可得∠CDV就是二面角V-AB-C的平面角.再由题中数据,分别算出VD、CD的长,可得△VCD是等边三角形,从而得到二面角V-AB-C的大小为60°.
解答: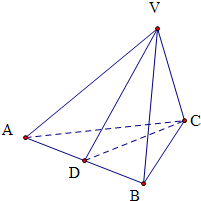 解:取AB的中点D,连结CD、VD
解:取AB的中点D,连结CD、VD
∵等腰三角形VAB中,VA=VB=2,D为AB中点
∴VD⊥AB
同理可得CD⊥AB,可得∠CDV就是二面角V-AB-C的平面角
Rt△VAD中,VD=
=1,同理可得CD=1
∵VC=1
∴△VCD是边长等于1的等边三角形,可得∠CDV=60°
因此,二面角V-AB-C的大小为60°
 解:取AB的中点D,连结CD、VD
解:取AB的中点D,连结CD、VD∵等腰三角形VAB中,VA=VB=2,D为AB中点
∴VD⊥AB
同理可得CD⊥AB,可得∠CDV就是二面角V-AB-C的平面角
Rt△VAD中,VD=
| VA2-AD2 |
∵VC=1
∴△VCD是边长等于1的等边三角形,可得∠CDV=60°
因此,二面角V-AB-C的大小为60°
点评:本题给出特殊三棱锥,求二面角的大小.着重考查了等腰三角形的性质、二面角的平面角的定义及其求法等知识,属于中档题.

练习册系列答案
相关题目
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4. 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.