题目内容
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC.(1)求证:AC⊥平面DEF;
(2)求平面DEF与平面ABD所成的锐二面角的余弦值;
(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.

【答案】分析:(1)要证AC⊥平面DEF,先证AC⊥DE,再证AC⊥EF,即可;
(2)分别计算面积,利用面积比,即可求平面DEF与平面ABD所成的锐二面角的余弦值;
(3)M为BD的中点,连CM,设CM∩DE=O,连OF,只要MN∥OF即可,求出CN.
解答: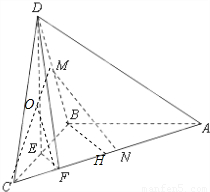 (1)证明:取AC的中点H,连接BH,
(1)证明:取AC的中点H,连接BH,
∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC,∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF;
(2)解:设AB=BC=2a,则DE=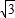 a,EF=
a,EF=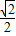 a,∴
a,∴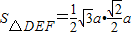 =
=
∵ =2a
=2a
∴平面DEF与平面ABD所成的锐二面角的余弦值为 ;
;
(3)解:存在这样的点N,
当CN= CA时,MN∥平面DEF.
CA时,MN∥平面DEF.
连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO= CM.
CM.
∴当CF= CN时,MN∥OF,∴CN=
CN时,MN∥OF,∴CN=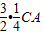 =
= CA
CA
点评:本题考查线面垂直,线面平行,考查面面角,考查逻辑思维能力,属于中档题.
(2)分别计算面积,利用面积比,即可求平面DEF与平面ABD所成的锐二面角的余弦值;
(3)M为BD的中点,连CM,设CM∩DE=O,连OF,只要MN∥OF即可,求出CN.
解答:
 (1)证明:取AC的中点H,连接BH,
(1)证明:取AC的中点H,连接BH,∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC,∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF;
(2)解:设AB=BC=2a,则DE=
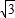 a,EF=
a,EF=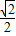 a,∴
a,∴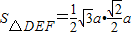 =
=
∵
 =2a
=2a∴平面DEF与平面ABD所成的锐二面角的余弦值为
 ;
;(3)解:存在这样的点N,
当CN=
 CA时,MN∥平面DEF.
CA时,MN∥平面DEF.连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO=
 CM.
CM.∴当CF=
 CN时,MN∥OF,∴CN=
CN时,MN∥OF,∴CN=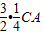 =
= CA
CA点评:本题考查线面垂直,线面平行,考查面面角,考查逻辑思维能力,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
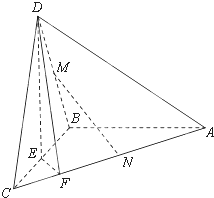 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.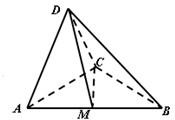 如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=
如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=

