题目内容

已知函数f（x）=x²-cosx，x∈ $数学公式$ ，则满足f（x₀）＞f（ $数学公式$ ）的x₀的取值范围为________．

$\text{[math]}$ ∪ $\text{[math]}$
分析：先充分考虑函数f（x）=x²-cosx，x∈ $\text{[math]}$ 的性质，为偶函数，其图象关于y轴对称，故考虑函数 $\text{[math]}$ 区间上的情形，利用导数可得函数在 $\text{[math]}$ 单调递增，再结合f（x₀）＞f（ $\text{[math]}$ ）和对称性即可得x₀的取值范围．
解答：注意到函数 $\text{[math]}$ 是偶函数故只需考虑 $\text{[math]}$ 区间上的情形．
由 $\text{[math]}$ 知函数在 $\text{[math]}$ 单调递增，
所以 $\text{[math]}$ 在 $\text{[math]}$ 上的解集为 $\text{[math]}$ ，
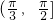结合函数是偶函数，图象关于y轴对称，得原问题中x₀取值范围是 $\text{[math]}$ ．
故答案为 $\text{[math]}$
点评：这是一个常见考型，应引起足够重视．填写答案时，应注意区间的闭、开问题，注意规范答题，否则将可能因为表述问题而失去已到手的分．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜

）的部分图象如图所示，则f（x）的解析式是（　　）

A、f(x)=2sin(πx+

B、f(x)=2sin(2πx+

C、f(x)=2sin(πx+

D、f(x)=2sin(2πx+

（2012•深圳一模）已知函数f(x)=

x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x

， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

（2011•上海模拟）已知函数f(x)=(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

已知函数f(x)=(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

已知函数f(x)=

x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x

， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．