Question

16．已知A，B分别是x轴和y轴上的点，且|$\overrightarrow{OA}$|=1，|$\overrightarrow{OB}$|=$\sqrt{3}$，点C落在∠AOB内，测得∠AOC=30°．若$\overrightarrow{OC}$=（m+1）$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R且m+n=3），则$\frac{m}{n}$=$\frac{1}{2}$．

Answer 1

分析 根据题意，建立平面直角坐标系，利用坐标表示$\overrightarrow{OC}$、$\overrightarrow{OA}$与$\overrightarrow{OB}$之间的关系，列出方程组求出$\frac{m}{n}$的值．

解答 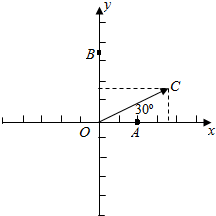解：建立如图所示的坐标系，
由已知数据得B（0，$\sqrt{3}$），A（1，0），
设C（x，y），则$\overrightarrow{OC}$=（x，y），$\overrightarrow{OA}$=（1，0），$\overrightarrow{OB}$=（0，$\sqrt{3}$），
由题意得（x，y）=（m+1）（1，0）+n（0，$\sqrt{3}$）=（m+1，$\sqrt{3}$n），
∴$\left\{\begin{array}{l}{x=m+1}\\{y=\sqrt{3}n}\\{m+n=3}\end{array}\right.$；
又$\frac{y}{x}$=$\frac{\sqrt{3}n}{m+1}$=tan30°=$\frac{\sqrt{3}}{3}$，
∴3n=m+1，即m=3n-1，
代入m+n=3中，解得m=1，n=2；
∴$\frac{m}{n}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查了平面向量的基本定理及其应用问题，解题时应建立平面直角坐标系，是中档题目．