题目内容
在直角坐标系xoy中，已知直线l的参数方程为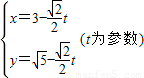
，圆C的参数方程为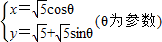
（1）求圆C的直角坐标方程；
（2）设圆C与直线l相交于A、B点，若P的坐标为
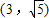，求|PA|+|PB|．
【答案】分析：（1）先利用三角函数中的平方关系消去参数θ即可得到圆C的普通方程，
（2）把直线参数方程代入圆的方程化简可得t2-3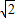
t+4=0，利用根与系数的关系，以及|PA|=|t1|，|PB|=|t2|求出|PA|+|PB|．
解答：解：（1）消去参数θ，得圆C的普通方程为：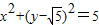
；
（2）将直线的参数方程带人圆的直角坐标方程，
得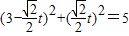
，
即t2-3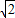
t+4=0，
由于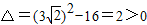
，
设t1，t2为方程两根，所以有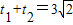
，t1•t2=4
由几何意义可得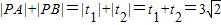
．
点评：本题考查参数方程化成普通方程，以及直线方程中参数的意义．属于基础题．
（2）把直线参数方程代入圆的方程化简可得t2-3
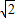t+4=0，利用根与系数的关系，以及|PA|=|t1|，|PB|=|t2|求出|PA|+|PB|．解答：解：（1）消去参数θ，得圆C的普通方程为：
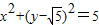；（2）将直线的参数方程带人圆的直角坐标方程，
得
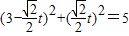，即t2-3
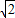t+4=0，由于
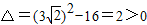，设t1，t2为方程两根，所以有
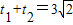，t1•t2=4由几何意义可得
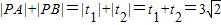．点评：本题考查参数方程化成普通方程，以及直线方程中参数的意义．属于基础题．
练习册系列答案
相关题目
如图所示，在直角坐标系xOy中，射线OA在第一象限，且与x轴的正半轴成定角60°，动点P在射线OA上运动，动点Q在y轴的正半轴上运动，△POQ的面积为