题目内容
18.若1-$\sqrt{2}$i(i是虚数单位)是关于x的实系数方程x2+bx+c=0的一个复数根,则( )| A. | b=2,c=3 | B. | b=2,c=-1 | C. | b=-2,c=-1 | D. | b=-2,c=3 |
分析 利用实系数一元二次的虚根成对原理、根与系数的关系即可得出.
解答 解:∵1-$\sqrt{2}$i是关于x的实系数方程x2+bx+c=0的一个复数根,
∴1+$\sqrt{2}$i是关于x的实系数方程x2+bx+c=0的一个复数根,
∴$\left\{\begin{array}{l}{1-\sqrt{2}i+1+\sqrt{2}i=-b}\\{(1-\sqrt{2}i)(1+\sqrt{2}i)=c}\end{array}\right.$,解得b=-2,c=3.
故选:D.
点评 本题考查了实系数一元二次的虚根成对原理、根与系数的关系,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
6.设θ是两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角,若对任意实数t,|$\overrightarrow{a}$+t$\overrightarrow{b}$|的最小值为1,则下列判断正确的是( )
| A. | 若|$\overrightarrow{a}$|确定,则θ唯一确定 | B. | 若|$\overrightarrow{b}$|确定,则θ唯一确定 | ||
| C. | 若θ确定,则|$\overrightarrow{b}$|唯一确定 | D. | 若θ确定,则|$\overrightarrow{a}$|唯一确定 |
3.在等比数列{an}中,a2=1,a6=9,则a4=( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $±\sqrt{3}$ |
7.在△OAB中,已知OA=5,OB=4,点P是AB的中点,则$\overrightarrow{OP}•\overrightarrow{AB}$=( )
| A. | 10 | B. | -$\frac{9}{2}$ | C. | 20 | D. | -20 |
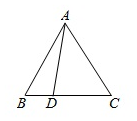 如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.
如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.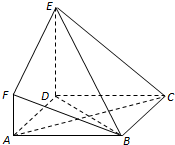 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.