题目内容
已知两定点A(-t,0)和B(t,0),t>0.S为一动点,SA与SB两直线的斜率乘积为(1)求动点S的轨迹C的方程,并指出它属于哪一种常见曲线类型;
(2)当t取何值时,曲线C上存在两点P、Q关于直线x-y-1=0对称?
解析:(1)设S(x,y),SA的斜率k1=![]() (x≠-t),
(x≠-t),
SB斜率k2=![]() (x≠t),
(x≠t),
由题意,得![]() (x≠±t),
(x≠±t),
经整理,得![]() -y2=1(x≠±t).
-y2=1(x≠±t).
点S的轨迹C为双曲线(除去两顶点).
(2)假设C上存在这样的两点P(x1,y1)和Q(x2,y2),
则PQ直线斜率为-1,且P、Q的中点在直线x-y-1=0上.设PQ直线方程为:y=-x+b,
由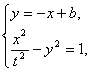 整理得(1-t2)x2+?2t2bx-t2b2-t2=0.
整理得(1-t2)x2+?2t2bx-t2b2-t2=0.
其中1-t2=0,方程只有一个解,与假设不符.
当1-t2≠0时,Δ>0,Δ=(2bt2)2-4(1-t2)(-t2b2-t2)=4t2(b2+1-t2),
所以t2<b2+1, ①
又x1+x2=-![]() ,
,
所以![]() .
.
代入y=-x+b,得![]() .
.
因为P、Q中点为(![]() )在直线x-y-1=0上,
)在直线x-y-1=0上,
所以有:-![]() -1=0,整理得t2=
-1=0,整理得t2=![]() , ②
, ②
解①②,得-1<b<0,0<t<1,经检验,得:当t取(0,1)中任意一个值时,曲线C上均存在两点关于直线x-y-1=0对称.

练习册系列答案
相关题目
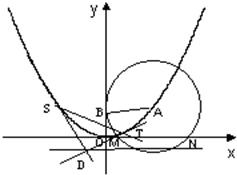 如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.
如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.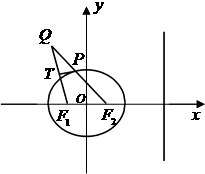 已知椭圆
已知椭圆 (a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),离心率为
(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),离心率为 ,椭圆上的动点P到直线l:x=
,椭圆上的动点P到直线l:x= 的最小距离为2,延长F2P至Q使得|
的最小距离为2,延长F2P至Q使得|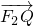 |=2a,线段F1Q上存在异于F1的点T满足
|=2a,线段F1Q上存在异于F1的点T满足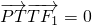 .
. ,满足
,满足 ,已知两定点A(1,0),B(-1,0),动点P(x,y),
,已知两定点A(1,0),B(-1,0),动点P(x,y),